Определение скоростей точек плоской фигуры

Было отмечено, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью 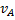полюса А, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически из скоростей, которые точка получает в каждом из этих движений.

В самом деле, положение любой точки М фигуры определяется по отношению к осям Оху радиусом-вектором (рис.30), где 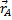- радиус-вектор полюса А, 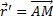- вектор, определяю­щий положение точки М относительно осей 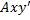, перемещающих­ся вместе с полюсом А поступательно (движение фигуры по отноше­нию к этим осям представляет собой вращение вокруг полюса А). Тогда

В полученном равенстве величина есть скорость полюса А; величина же 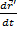равна скорости , которую точка М получает при 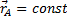, т.е. относительно осей , или, иначе говоря, при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что

.

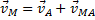Скорость , которую точка М получает при вращении фигуры вокруг полюса А:

,

где ω - угловая скорость фигуры.

Таким образом, скорость любой точки М плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление скорости 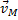находятся построением соответствующего параллело­грамма (рис.31).

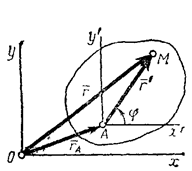
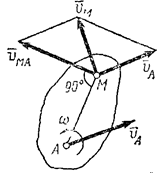
Рис.30 Рис.31

Date: 2015-09-03; view: 338; Нарушение авторских прав