Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей

Другой простой и наглядный метод определения скоростей точек плоской фигуры (или тела при плоском движении) основан на поня­тии о мгновенном центре скоростей.

Мгновенным центром скоростей называется точка плоской фигу­ры, скорость которой в данный момент времени равна нулю.

Легко убедиться, что если фигура движется непоступательно, то такая точка в каждый момент времени t существует и притом единственная. Пусть в момент времени t точки А и В плоской фигуры имеют скорост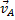и и 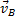, не параллельные друг другу (рис.33). Тогда точка Р, лежащая на пересечении перпендикуляров Аа к вектору 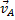и Вb к вектору 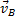, и будет мгновенным центром скоростей так как 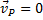. В самом деле, если допустить, что 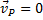, то по теореме о проекциях скоростей вектор 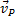должен быть одновременно перпендикулярен и АР (так как 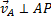) и ВР (так как 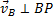), что невозможно. Из той же теоремы видно, что никакая другая точ­ка фигуры в этот момент времени не может иметь скорость, равную нулю.

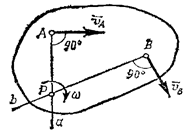
Рис.33

Если теперь в момент времени 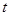взять точку Р за полюс, то скорость точки А будет

,

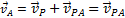так как 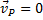. Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом

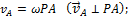
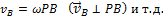
Из равенств, следует еще, что

точек плоской фигуры пропорциональны их расстоя­ниям от МЦС.

Полученные результаты приводят к следующим выводам.

1. Для определения мгновенного центра скоростей надо знать то­лько направления скоросте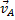й и 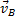каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, вос­ставленных из точек А и В к скоростям этих точек (или к каса­тельным к траекториям).

2. Для определения скорости любой точки плоской фигуры, надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В. Тогда, вос­ставив из точек А и В перпендикуляры к 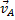и 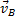, построим мгно­венный центр скоростей Р и по направлению 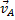определим направ­ление поворота фигуры. После этого, зная 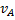, найдем скорость 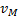любой точки М плоской фигуры. Направлен век­тор 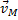перпендикулярно РМ в сторону поворота фигуры.

3. Угловая скорость плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р:

.

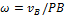Рассмотрим некоторые частные случаи определения мгновенного центра скоростей.

а) Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверх­ности другого неподвижного, то точка Р катящегося тела, касаю­щаяся неподвижной поверхности (рис.34), имеет в данный момент времени вследствие отсутствия скольжения скорость, равную нулю (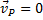), и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу.

б) Если скорости точек А и В плоской фигуры параллельны друг другу, причем линия АВ не перпендикулярна 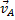(рис.35,а), то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны 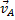. При этом из теоремы о проекциях скоростей следует, что 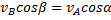т. е. 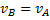; аналогичный результат получается для всех других точек. Следовательно, в рас­сматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступа­тельным). Угловая скорость тела в этот момент времени, как видно равна нулю.

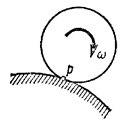
Рис.34

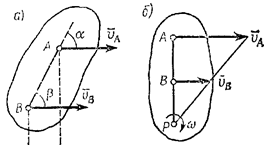
Рис.35

в) Если скорости точек А и В плоской фигуры параллельны друг другу и при этом линия АВ перпендикулярна 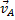, то мгновен­ный центр скоростей Р определяется построением, показанным на рис. 35,б. Справедливость построений следует из пропорции. В этом случае, в отличие от предыдущих, для нахождения центра Р надо кроме направлений знать еще и модули скоростей .

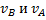г) Если известны вектор скорости 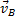какой-нибудь точки В фигуры и ее угловая скорость , то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к 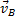(рис.35,б), можно найти как .

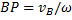Date: 2015-09-03; view: 440; Нарушение авторских прав