Решение задач на определение ускорения

Ускорение любой точки плоской фигуры в данный момент времени можно найти, если известны: 1) векторы скорости 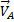и ускорения 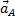какой-нибудь точки А этой фигуры в данный момент; 2) траектория какой-нибудь другой точки В фи­гуры. В ряде случаев вместо траектории второй точки фигуры до­статочно знать положение мгновенного центра скоростей.

Тело (или механизм) при решении задач надо изображать в том положении, для которого требуется определить ускорение соответ­ствующей точки. Расчет начинается с определения по данным задачи скорости и ускорения точки, принимаемой за полюс.

План решения (если заданы скорость и ускорение одной точки плоской фигуры и направления скорости и ускорения другой точки фигуры):

1) Находим мгновенный центр скоростей, восставляя перпендикуляры к скоростям двух точек плоской фигуры.

2) Определяем мгновенную угловую скорость фигуры.

3) Определяем центростремительное ускорение точки вокруг полюса, приравнивая нулю сумму проекций всех слагаемых ускорений на ось, перпендикулярную к известному направлению ускорения.

4) Находим модуль вращательного ускорения, приравнивая нулю сумму проекций всех слагаемых ускорений на ось, перпендикулярную к известному направлению ускорения.

5) Определяем мгновенное угловое ускорение плоской фигуры по найденному вращательному ускорению.

6) Находим ускорение точки плоской фигуры при помощи формулы распределения ускорений.

При решении задач можно применять «теорему о проекциях векторов ускорений двух точек абсолютно твердого тела»:

«Проекции векторов ускорений двух точек абсолютно твердого тела, которое совершает плоскопараллельное движение, на прямую, повернутую относительно прямой, проходящей через эти две точки, в плоскости движения этого тела на угол 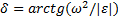в сторону углового ускорения, равны».

Эту теорему удобно применять, если известны ускорения только двух точек абсолютно твердого тела как по модулю, так и по направлению, известны только направления векторов ускорений других точек этого тела (геометрические размеры тела не известны), не известны и 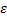– соответственно проекции векторов угловой скорости и углового ускорения этого тела на ось, перпендикулярную плоскости движения, не известны скорости точек этого тела.

Известны еще 3 способа определения ускорений точек плоской фигуры:

1) Способ основан на дифференцировании дважды по времени законов плоскопараллельного движения абсолютно твердого тела.

2) Способ основан на использовании мгновенного центра ускорений абсолютно твердого тела (о мгновенном центре ускорений абсолютно твердого тела будет рассказано ниже).

3) Способ основан на использовании плана ускорений абсолютно твердого тела.

Пример 11. Диск катится без скольжения по прямой. Центр его С имеет скорость 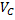и ускорение 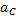(рис. 43). Найдем ускорение точки А.

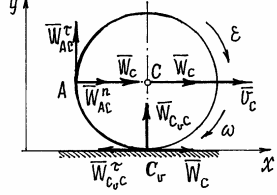
Рис.43

Угловую скорость находим с помощью мгновенного центра скоростей:

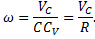
Угловое ускорение при таком движении можно найти как производную от угловой скорости. Имея в виду, что 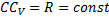, а точка С движется по прямой, получим

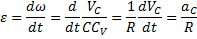
Если С – полюс, то 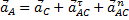, где

.

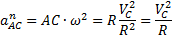
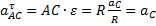Величину ускорения найдём с помощью проекций на оси х и у:

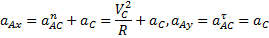
Ускорение мгновенного центра скоростей ,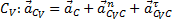

где .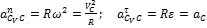

И, так как 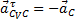, ускорение 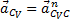и .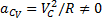

Таким образом, ускорение мгновенного центра скоростей не равно нулю.

Пример 12. Вернёмся к примеру 9 (рис. 44).

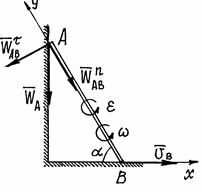
Рис.44

Найдём ускорение точки А, полагая 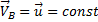т.е.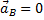

Имеем:

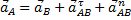, (1)

Где , но направление вектора 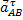неизвестно, неизвестно и угловое ускорение .

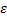Предположим, что вектор 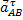направлен перпендикулярно АВ, влево.

Ускорение 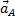, конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим:

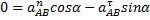и .

Из второго уравнения сразу находим ускорение точки А

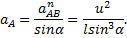
Положительное значение 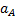указывает на то, что направление вектора 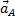выбрано правильно.

Из первого уравнения можно найти ускорение 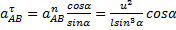и угловое ускорение 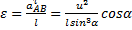(направления 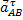и 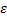также угаданы верно).

Date: 2015-09-03; view: 385; Нарушение авторских прав