
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение. 1) У точек находящихся на колесе и лежащих на радиусе, будут одинаковы угловые скорости
|
|
1) У точек находящихся на колесе и лежащих на радиусе, будут одинаковы угловые скорости. Используем связь угловой и линейной скоростей:

т.к. ω1=ω2, приравниваем правые части уравнений:

Решим уравнение относительно R:


Ответ: Радиус вращающегося колеса равен 8,33 см.
Пример 13. На рис.28 показаны направления вращения гироскопа (волчка) и указано, увеличивается или уменьшается угловая скорость. Укажите номер рисунка, на котором правильно указано направление углового ускорения.
| e |
| w увеличивается |
| e |
| w уменьшается |
| e |
| w уменьшается |
| w увеличивается |
| e |
Рис.28
Решение. Псевдовектор угловой скорости связан с направлением вращения правилом буравчика (правого винта). На рис.28.1 и рис.28.3 он направлен вверх, на рис.28.2 и рис.28.4 - вниз.
При возрастании угловой скорости ее приращение, а соответственно и вектор углового ускорения совпадают с вектором угловой скорости (рисунки 1 и 4). При уменьшении угловой скорости ее приращение, а соответственно и вектор углового ускорения противоположны вектору угловой скорости (рис.28.2 и рис.28.3). Следовательно, на всех рисунках направление углового ускорения указано правильно.
Пример 14. Опишите движение вращающегося твердого тела в случаях, когда угловая скорость изменяется согласно графикам 1 и 2, изображенным на рис.29.
| w |
| t |
Рис.29
Решение. Начнем с того, что вращение бывает в двух направлениях - по часовой стрелке и против. С направлением вращения связан псевдовектор угла поворота и угловой скорости. Пусть положительным будем считать направление вращения по часовой стрелке.
Для движения 1 угловая скорость возрастает, но угловое ускорение ε=dω/dt (производная) уменьшается, оставаясь положительным. Следовательно, это движение является ускоренным по часовой стрелке с уменьшающимся по величине ускорением.
Для движения 2 угловая скорость уменьшается, затем достигает в точке пересечения с осью абсцисс нуля, а далее становится отрицательной и возрастает по модулю. Угловое ускорение (вспомните геометрический смысл производной) отрицательно и уменьшается по модулю. Таким образом, сначала точка двигалась по часовой стрелке замедленно с уменьшающимся по модулю угловым ускорением, остановилась и стала вращаться ускоренно с уменьшающимся по модулю ускорением (оба вектора - и угловая скорость, и угловое ускорение направлены в одну сторону).
Пример 15. Скорость точки, движущейся по кривой, уменьшается по модулю. На каком рисунке, показанных на рис.30 правильно показан вектор полного ускорения?
| v |
| v |
| v |
| v |
| a |
| a |
| a |
| a |
Рис.30
Решение. При движении по криволинейной траектории скорость изменяется по величине и направлению. Составляющая ускорения, характеризующая быстроту изменения скорости по величине, называется тангенциальным ускорением. Она связана с приращением вектора скорости, направленным по касательной к траектории, как и сама скорость. При ускоренном движении тангенциальная составляющая совпадает с вектором скорости, при замедленном - противоположна (как на рис.30.1)
Составляющая ускорения, характеризующая быстроту изменения скорости по направлению, называется нормальным ускорением. Она связана с приращением вектора скорости, направленным перпендикулярно касательной к траектории. Нормальное ускорение всегда направлено к центру кривизны траектории (как на рис. 30.3)
Вектор полного ускорения  правильно изображен на рис.30.2.
правильно изображен на рис.30.2.
Пример 16. Угловая скорость точки, движущейся по окружности, изменяется по графику, изображенному на рис.31. Как изменяется со временем угол между векторами ускорения и скорости?
| w |
| t |
Рис.31
Решение. Согласно графику угловая скорость линейно возрастает. Угловое ускорение по определению равно производной угловой скорости по времени ε=dω/dt.
Производная линейной функции постоянна, поэтому угловое ускорение не изменяется.
Запишем выражения, связывающие составляющие ускорения с угловыми величинами: 
Следовательно, тангенциальное ускорение не изменяется по величине в процессе движения, а нормальное ускорение возрастает.
Построим векторы скорости, нормального, тангенциального и полного ускорений. Вектор скорости направлен по касательной к траектории. Направление вектора ускорения рассматривалось ранее.
| a |
| an |
| at |
| v |
| a |
Рис.32
Из рис.32 видно, что угол α между векторами скорости и ускорения возрастает.
Пример 17. Точка движется, замедляясь, по окружности радиуса R так, что в каждый момент времени ее тангенциальное и нормальное ускорения по модулю равны друг другу. В начальный момент времени t = 0 скорость точки равна v 0. Найти скорость и ускорение точки как функцию времени.
Решение. Установим уравнения, связывающие аn и аτ. По условию задачи модули нормального и тангенциального ускорений совпадают: |an|=|aτ|. Нормальное ускорение всегда положительно. При замедленном движении приращение скорости отрицательно. С учетом этих замечаний система уравнений принимает вид
аn=-а τ, (1)


Подставляя (2) и (3) в (1), приходим к уравнению с разделяющимися переменными:

Разделяя переменные v и t, получаем

Интегрируем в пределах от t = 0, v = v 0 до t и v(t)
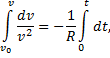
в результате имеем:

Из этого соотношения находим искомую зависимость скорости от времени

Подставляем v(t) в формулу (2)

Учитывая, что an=-aτ и  , получаем зависимость полного ускорения от времени:
, получаем зависимость полного ускорения от времени:
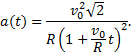
Пример 18. Материальная точка движется по окружности радиуса R так, что зависимость угла поворота от времени задана уравнением φ=αt3. Найти полное ускорение точки как функцию времени.
Решение. Решим задачу двумя способами.
1 способ. Выпишем формулы соответствующие данному способу.



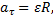
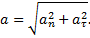
Выполним указанные в формулах математические действия.


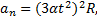


2 способ. Выпишем формулы соответствующие данному способу.
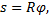
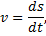


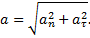
Выполним указанные в формулах математические действия.





Вопросы для самопроверки
- Что определяет число степеней свободы твердого тела?
- Какими кинематическими параметрами характеризуется поступательное движение и почему?
- Запишите уравнение равномерного поступательного движения твердого тела?
- Запишите уравнение равнопеременного поступательного движения твердого тела?
- Запишите уравнение равнопеременного и равномерного вращательного движения твердого тела?
- Почему при поступательном движении тела скорости и ускорения его точек не могут быть различными?
- Сколько степеней свободы имеет тело с двумя закрепленными точками?
- Приведите определения угловой скорости и углового ускорения тела.
- Как направлены векторы угловой скорости и углового ускорения при вращении тела вокруг неподвижной оси?
- Как вычислить скорость точки тела, вращающегося вокруг неподвижной оси? Объясните куда направлен вектор скорости?
- Запишите формулы для нормального и тангенциального ускорений точки тела, вращающегося вокруг неподвижной оси.
- Перечислите основные виды движений твердого тела.
- Какое движение твердого тела называется поступательным и какими свойствами оно обладает?
- Какое движение твердого тела называется вращением вокруг неподвижной оси и как оно осуществляется?
- По каким формулам определяются модули угловой скорости и углового ускорения вращающегося твердого тела?
- Как направлены векторы угловой скорости и углового ускорения при вращении тела вокруг неподвижной оси?
- Выведите формулы модулей скорости и ускорения точек твердого тела, вращающегося вокруг неподвижной оси?
- При каких условиях ускорение точки вращающегося тела составляет с отрезком, соединяющим точку с центром описываемой ею окружности, углы 00, 450, 900?
- Ускорения каких точек вращающегося тела:
а) равны по модулю;
б) совпадают по направлению;
в) равны по модулю и совпадают по направлению?
- Каковы векторные выражения вращательной скорости, вращательного и центростремительного ускорений?
- Выведите формулы Эйлера для проекций вращательно скорости точки на координатные оси.
- Что представляет собой передаточное число передачи и как определяется передаточное число сложной передачи?
- На какие составляющие движения можно разложить движение свободного тела в общем случае и как они зависят от выбора полюса?
- Как определяют скорости точек свободного твердого тела?
- Как связаны между собой скорости точек свободного тела, расположенных на отрезке произвольного направления, и на отрезке, параллельном мгновенной оси?
- Покажите, что векторы угловой скорости и углового ускорения свободного тела не зависят от выбора полюса.
- Как определяют ускорения точек свободного твердого тела?
- Чему равно число степеней свободы тела с одной закрепленной точкой?
- Приведите названия углов Эйлера.
- Запишите уравнения вращения твердого тела вокруг неподвижной точки.
- Сформулируйте теорему Эйлера-Даламбера.
- Что определяют кинематические уравнения Эйлера?
- Приведите векторную запись формулы для определения линейной скорости точки при вращении твердого тела с одной неподвижной точкой.
- Как определить величину и направление вращательного ускорения точки твердого тела с одной закрепленной точкой?
- Как направлен вектор осестремительного ускорения точки при вращении твердого тела вокруг неподвижной точки?
- Какими параметрами определяется положение твердого тела, одна из точек которого неподвижна?
- Как формулируется теорема Эйлера-Даламбера о перемещении твердого тела, имеющего одну неподвижную точку?
- Что называют мгновенной осью вращения твердого тела с одной неподвижной точкой и каковы уравнения мгновенной оси в неподвижной и подвижной системах осей декартовых координат?
- Что представляют собой неподвижный и подвижный аксоиды мгновенных осей при сферическом движении и что происходит с аксоидами при действительном движении тела?
- Как определяются модуль и направление углового ускорения тела при сферическом движении?
- Почему направления векторов углового ускорения и угловой скорости тела при сферическом движении не совпадают?
- Как определяются скорости точек тела при сферическом движении?
- Какие модули и направления имеют составляющие ускорения точки тела при сферическом движении?
- Почему направления векторов вращательной скорости и вращательного ускорения при сферическом движении тела не совпадают?
- Определите угловую скорость вращения вала электродвигателя (в рад/с), если n =1400 об/мин.? Вычислите скорость и ускорение точки на поверхности вала; диаметр вала d =100 мм?
- Определите характер вращения твердого тела вокруг неподвижной оси в следующих случаях:
1) ε=5 рад/с2;
2) ε=0;
3) ω=150 рад/с;
4) ω=20 t рад/с, где t – время?
- Какая составляющая ускорения любой точки твердого тела равна нулю при равномерном вращении твердого тела вокруг неподвижной оси?
1) нормальное ускорение;
2) касательное ускорение;
3) полное ускорение.
Date: 2015-09-03; view: 2567; Нарушение авторских прав