Скорости и ускорения точек вращающегося тела

Установив характеристики движения всего тела в целом, перейдем к изучению движения отдельных его точек.

1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис.9). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время dt проис­ходит элементарный поворот тела на угол dφ, то точка М при этом совершает вдоль своей траектории элементарное перемещение ds=hdφ. Тогда числовое значение скорости точки будет равно отно­шению ds к dt, т.е

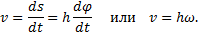
Скорость 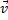в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.

Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстоя­ние от этой точки до оси вращения.

Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.

Так как для всех точек тела имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.

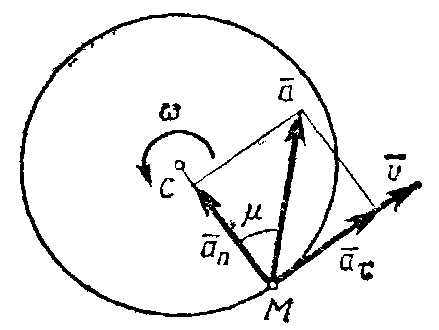
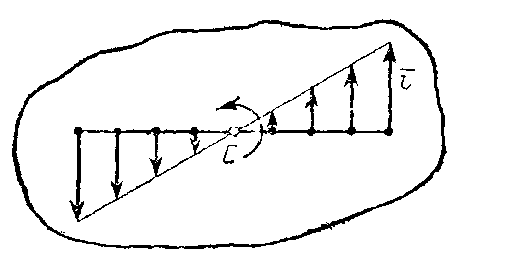
Рис.11 Рис. 12

2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами

В нашем случае ρ=h. Подставляя значение v в выражения a_τ и a_n, получим:

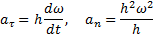
или окончательно:

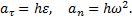
Касательная составляющая ускорения a_τ направлена по каса­тельной к траектории (в сторону движения при ускоренном вра­щении тела и в обратную сторону при, замедленном); нормальная составляющая a_n всегда направлена по радиусу МС к оси вращения (рис.12). Полное ускорение точки М будет

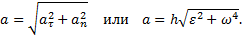
Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом μ, который вычисляется по формуле

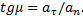
Подставляя сюда зна­чения a_τ и a_n, получаем

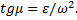
Так как ω и ε имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональ­ны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол μ с радиусами описываемых ими окруж­ностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.14.

Рис.13 Рис.14

3. Векторы скорости и ускорения точек тела. Чтобы найти выражения непосредственно для векторов v и a, проведем из произвольной точки О оси АВ радиус-вектор точки М (рис. 13). Тогда h=r∙sinα и по формуле

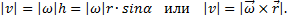
Таким образом, модуль векторного произведения равен модулю скорости точки М. Направления векторов и v тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерно­сти их одинаковы. Следовательно, - формула Эйлера, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.

Пример 1. Маятник OM качается в вертикальной плоскости так, что φ=0,5sin2t. Длина OM= l =1м. (рис. 15).

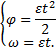
Рис.15

Решение. Маятник вращается вокруг горизонтальной оси О, перпендикулярной вертикальной плоскости. Угловая скорость 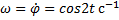угловое ускорение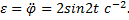

Например, при t=1 с, φ=0,5sin2=0,45 рад≅26°; ω=cos2=-0,42 c^-1 (вращение по часовой стрелке); ε=-2sin2=-1,82 c^-2 (угловое уско­рение направлено также по часовой стрелке). Вращение в этом положении ускоренное.

Скорость точки M: v_M= l ω=1∙0,42=0,42 м∙с^-1 (определя­ется модуль скорости). Направлен вектор скорости соответственно направлению угловой скорости – в сторону вращения.

Величина полного ускорения точки

Date: 2015-09-03; view: 829; Нарушение авторских прав