
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Частные производные и дифференциалы
|
|
Пусть дана z=f(x;y). Дадим переменной х приращение  х. Тогда функция z=f(x;y) получит некоторое приращение только за счет приращения х. Обозначим его значком
х. Тогда функция z=f(x;y) получит некоторое приращение только за счет приращения х. Обозначим его значком  хz и назовем частным приращением. Естественно,
хz и назовем частным приращением. Естественно,  хz= f(x+
хz= f(x+  х;y)- f(x;y). Аналогичные приращения можно записать при изменении других переменных.
х;y)- f(x;y). Аналогичные приращения можно записать при изменении других переменных.
Опред. Частной производной от функции по данному аргументу называют предел отношения частного приращения функции к вызвавшеме его приращению аргумента, если последнее стремится к нулю.
Символически это факт записывают по разному: z’x; f’x;  ;
; 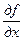 ;
; 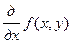 и т.д. Обратите внимание – в третьей и четвертой записях не записано отношение, а записан один символ! Читается всегда так ”частная производная от … по …”. Неверно читать “ дэ от … по дэ…”.
и т.д. Обратите внимание – в третьей и четвертой записях не записано отношение, а записан один символ! Читается всегда так ”частная производная от … по …”. Неверно читать “ дэ от … по дэ…”.
Распространим на частую производную известный геометрический ее смысл – частная производная характеризуют скорость изменения функции в направлении выбранной координатной оси.
Теорема(необходимое условие существования ЧП). Если f(x;y) имеет ЧП в данной точке, то функция непрерывна в этой точке.
Док. По определению f’x = 
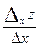 . Используя связь предела с бесконечно малой величиной получим
. Используя связь предела с бесконечно малой величиной получим  хz= f’x
хz= f’x  х+
х+ 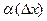
 х. Если теперь подсчитать пределы обеих частей полученного равенства, то получим одно из определений непрерывной в точке функции.
х. Если теперь подсчитать пределы обеих частей полученного равенства, то получим одно из определений непрерывной в точке функции.
Опред. Главная часть частного приращения функции, линейная относительно частного приращения аргумента называется частным дифференциалом функции и обозначается dxz= f’x  х или dxz= f’x dх.
х или dxz= f’x dх.
Пусть дана f(x;y). При переходе от точки М к точке Мо эта функция получит приращение  z, которое в отличие от частного следует называть полным приращением функции.
z, которое в отличие от частного следует называть полным приращением функции.
Опред. Если  z удается представить в виде А
z удается представить в виде А  х+В
х+В  у+
у+ 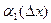
 х+
х+ 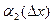
 у, то говорят, что z=f(x;y) дифференцируема, а выражение А
у, то говорят, что z=f(x;y) дифференцируема, а выражение А  х+В
х+В  у называют полным дифференциалом и обозначают dz.
у называют полным дифференциалом и обозначают dz.
Выведем формулу для вычисления полного дифференциала. Имеем  z= =f(x+
z= =f(x+  х;y+
х;y+  у)- f(x;y)= f(x+
у)- f(x;y)= f(x+  х;y+
х;y+  у) - f(x;y+
у) - f(x;y+  у) + f(x;y+
у) + f(x;y+  у) - f(x;y)= f(x+
у) - f(x;y)= f(x+  х;y+
х;y+  у)- f(x;y+
у)- f(x;y+  у) +(f(x;y+
у) +(f(x;y+  у)- f(x;y)). Для каждой разности применим формулу Лагранжа конечных отношений и получим
у)- f(x;y)). Для каждой разности применим формулу Лагранжа конечных отношений и получим  z= f’x(C1;y+
z= f’x(C1;y+  у)
у)  х+ f’y(x;C2)
х+ f’y(x;C2)  у, где точки C1 и C2 расположены на участках приращения переменных. Но, т.к.
у, где точки C1 и C2 расположены на участках приращения переменных. Но, т.к. 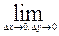 f’x(C1;y+
f’x(C1;y+  у)= f’x(х;y) и
у)= f’x(х;y) и 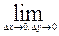 f’y(x;C2) = f’у(х;y), то из связи пределов с бесконечно малыми получаем
f’y(x;C2) = f’у(х;y), то из связи пределов с бесконечно малыми получаем
 z= f’x(х;y)
z= f’x(х;y)  х+ f’у(х;y)
х+ f’у(х;y)  у+
у+ 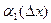
 х+
х+ 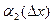
 у (5.1)
у (5.1)
Отсюда видно, что dz= А  х+В
х+В  у= f’x(х;y)
у= f’x(х;y)  х+ f’у(х;y)
х+ f’у(х;y)  у= f’x(х;y)dх+ f’у(х;y)d у. Т.е. полный дифференциал равен сумме частных дифференциалов.
у= f’x(х;y)dх+ f’у(х;y)d у. Т.е. полный дифференциал равен сумме частных дифференциалов.
Полный дифференциал удобно применять в вычислениях.
Пример 5.1. Вычислите приближенно 1,01 2,03. Решение. Подберем подходящую по виду функцию z=xy. Возьмем точку Мо достаточно близкую к точке М(1,01; 2,03) и такую, чтобы легко можно было вычислить значение функции в этой точке. Такой будет Мо(1;2). Тогда z(Мо)=1. При переходе от точки Мо к точке М функция получит некоторое приращение  z, которое мы не знаем. Но можем вычислить приближенно, заменив полным дифференциалом dz(Mo). Получаем
z, которое мы не знаем. Но можем вычислить приближенно, заменив полным дифференциалом dz(Mo). Получаем  z=dz= f’x(х;y)
z=dz= f’x(х;y)  х+ f’у(х;y)
х+ f’у(х;y)  у. Найдем частные производные функции в точке Мо. f’x(Мо) = y xy-1 =1. f’y(Мо) =xylnx=0.
у. Найдем частные производные функции в точке Мо. f’x(Мо) = y xy-1 =1. f’y(Мо) =xylnx=0.
 х=1,01-1=0,01;
х=1,01-1=0,01;  у=2,03-2=0,03. Получаем
у=2,03-2=0,03. Получаем  z=1(0,01)+0(0,03)=0,01. Окончательно 1,01 2,03 =1+0,01=1,01.
z=1(0,01)+0(0,03)=0,01. Окончательно 1,01 2,03 =1+0,01=1,01.
Date: 2015-09-02; view: 413; Нарушение авторских прав