И их систем

Если дано линейное дифференциальное уравнение 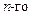порядка с постоянными коэффициентами

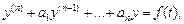
правая часть которого является оригиналом, то и решение этого уравнения, удовлетворяющее произвольным начальным условиям вида

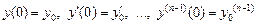
(т. е. решение задачи Коши), является оригиналом. Обозначая изображение этого решения через 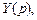находим изображение левой части исходного дифференциального уравнения и, приравнивания его к изображению функции 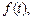приходим к так называемому изображающему уравнению, которое всегда является линейным алгебраическим уравнением относительно 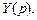Определив из этого уравнения 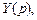находим оригинал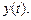

Пример 1. Решить задачу Коши

(30.41)

если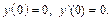

Решение. Обозначим через изображение функции Ис­пользуя формулу (30.21) и изображение оригинала 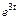(см. табл. 30.1), получаем

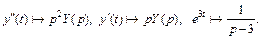
Согласно свойству линейности имеем

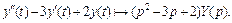
Вместе с тем по формуле (30.41),

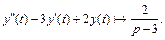
Это значит, что

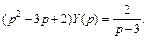
Из последнего уравнения находим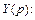

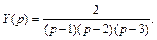
Разложим полученную дробь на сумму простейших дробей:

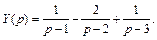
Снова используем формулу

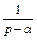
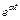
(см. формулу 3, табл. 30.1), и получаем

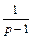
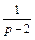
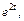
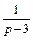
Искомое решение имеет вид

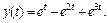
Пример 2. Решить задачу Коши

если

Решение. Используя формулу (30.20), получаем

В результате приходим к уравнению

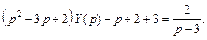
Отсюда находим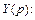

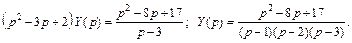
Раскладываем полученную дробь на сумму простейших:

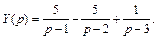
Отсюда следует, что искомое решение имеет вид

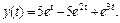
Пример 3. Решить задачу Коши

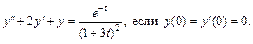
Решение. В основу решения положен метод, который базируется на формуле Дюамеля. Рассмотрим дополнительную задачу Коши:

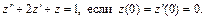
Будем считать, что 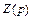где 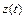− решение последнего дифференциального уравнения с данными начальными условиями. Теперь перейдем к изображениям. Левой части последнего дифференциального уравнения соответствует величина

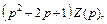
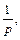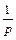
а правой части – величина где 1.

Получаем

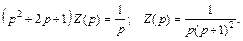(30.42)

Раскладываем полученную дробь на сумму простейших дробей:

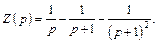
Используя табл. 30.1, находим (см. формулу (30.22))

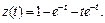
Заметим, что по условию имеем

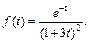
Пусть 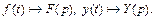Тогда для исходной задачи получим равенство

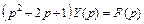
или (см. (30.42))

.

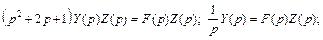
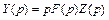На основе формулы Дюамеля (30.24) имеем

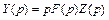
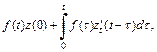
а поскольку (по условию), то

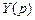
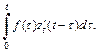
Вместе с тем 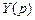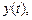а поэтому справедлива формула

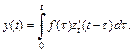(30.43)

Так как 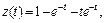то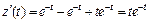

и формула (30.43) принимает вид

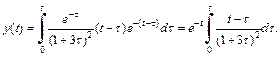
Вычисляя интеграл, находим

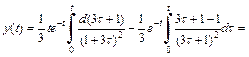
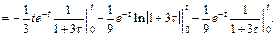
Подставив значения пределов интегрирования и сделав преобразования, приходим к ответу

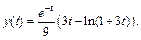
Пример 4. Решить задачу Коши

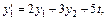
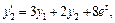если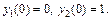

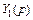
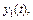
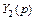
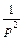
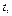
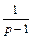
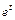Решение. Пусть Заметим также, что (см. табл. 30.1). Тогда соответствующая операторная система имеет вид

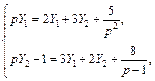или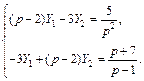

Решим эту систему методом Крамера, для чего найдем определители:

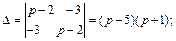
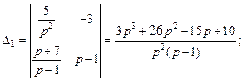
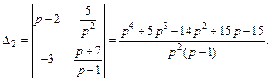
Тогда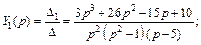

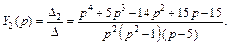
Для нахождения оригиналов 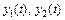используем формулу (30.33). Получим

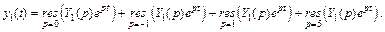Используя формулы (30.36) и (30.37), найдем вычеты: в точке 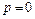− как в полюсе 2-го порядка, а в точках 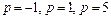− как в простых полюсах. Получаем

Аналогично

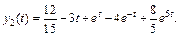
Пример 5. Решить систему дифференциальных уравнений второго порядка операционным методом:

Решение. Ищем решение задачи Коши, т. е. функции 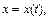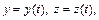которые считаем оригиналами. Пусть

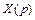
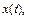
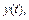
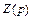
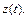
Учитывая начальные условия (см. формулу (30.20)), выполним переход от заданной системы дифференциальных уравнений к системе операторных уравнений, получим

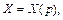
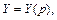
Решим эту систему относительно функций 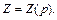Из последнего уравнения системы имеем

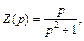(30.44)

и это выражение подставляем в первое уравнение:

Найдя 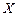из второго уравнения и подставив в первое, получим решение

Соответствующие оригиналы 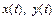для изображений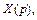 можно найти по формуле (30.33). В частности,

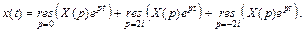
Вычислив эти вычеты (в полюсе второго порядка 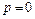и в простых полюсах 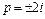), получим

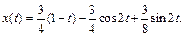
Аналогично

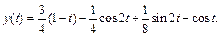
Из формулы (30.44) находим (см. табл. 30.1),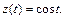

Date: 2015-09-02; view: 527; Нарушение авторских прав