
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференцирование оригиналов и изображений
|
|
Для дифференцирования оригиналов и изображений справедливы следующие теоремы.
Теорема 3 (о производной оригинала). Если  и
и 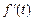 − оригиналы и
− оригиналы и 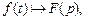 то верна формула
то верна формула
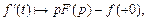 (30.19)
(30.19)
где 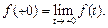
Далее будем обозначать 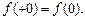
С л е д с т в и е. Если 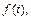
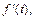
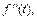 …,
…, 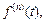
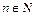 − оригиналы и
− оригиналы и 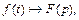 то справедлива формула
то справедлива формула
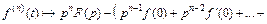
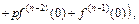 (30.20)
(30.20)
где 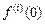 понимается аналогично
понимается аналогично 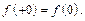
В частном случае, когда
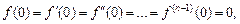
соотношение формулы (30.20) приобретает вид
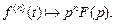 (30.21)
(30.21)
Теорема 4 (о производной изображения). Если 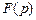

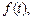 то верна формула
то верна формула
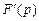

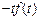 (30.22)
(30.22)
С л е д с т в и е. Если 

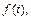 то справедлива формула
то справедлива формула
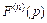

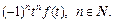 (30.23)
(30.23)
Теорема 5. Пусть 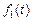 − непрерывный оригинал,
− непрерывный оригинал, 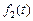 − оригинал с непрерывной производной
− оригинал с непрерывной производной 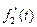 и
и 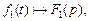
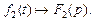 Тогда справедлива формула Дюамеля
Тогда справедлива формула Дюамеля
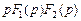

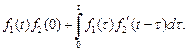 (30.24)
(30.24)
Теорема 6. Если функция  и ее производная
и ее производная 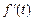 являются оригиналами и
являются оригиналами и 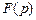

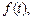 то
то
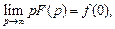 (30.25)
(30.25)
где 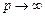 внутри угла
внутри угла 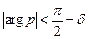 (
(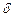 − произвольный малый угол,
− произвольный малый угол, 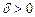 ) и
) и 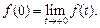
Если же 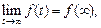 то
то
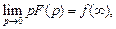 (30.26)
(30.26)
где 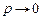 внутри угла
внутри угла 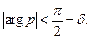
Пример 1. Пусть 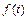 − оригинал,
− оригинал, 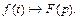 Найти изображение
Найти изображение  для функции
для функции 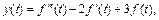 если
если 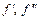 − оригиналы, причем
− оригиналы, причем 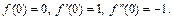
Решение. Согласно формуле (30.20), имеем
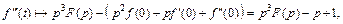
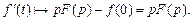
Свойство линейности, формула (30.4), приводит к соотношению
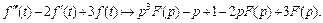
Получаем
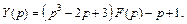
Пример 2. Найти изображение оригинала 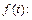
1) 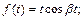 2)
2) 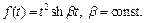
Решение. Используем формулы (30.22), (30.23), записав их в виде
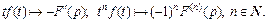
1) Согласно формуле (30.16), имеем
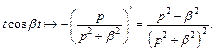
2) Применяя формулы (30.5) и (30.14), находим
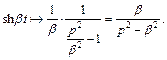 Тогда
Тогда
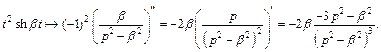
Значит,
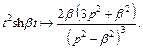
Пример 3. Найти изображение функции 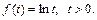
Решение. Обозначим искомое изображение через 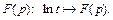
Согласно формуле дифференцирования изображения (30.22), имеем 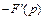

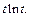 Используя свойство линейности, формула (30.4), и соотношение
Используя свойство линейности, формула (30.4), и соотношение
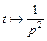 (см. пример 2, параграф 30.1, с. 7 данного пособия), находим
(см. пример 2, параграф 30.1, с. 7 данного пособия), находим
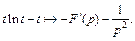
Продифференцируем оригинал в соответствии с формулой (30.19):
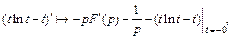
причем, согласно правилу Лопиталя, имеем
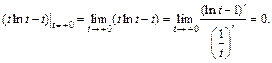
Поэтому получаем
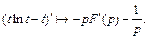
Так как 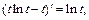 то имеем соотношение
то имеем соотношение
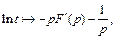 которое означает
которое означает
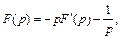 так как
так как 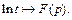
Из последнего равенства найдем 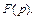 Очевидно, что
Очевидно, что
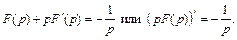
Выполнив интегрирование
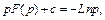
найдем 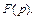
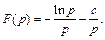 (30.27)
(30.27)
(рассматриваем только главное значение 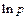 логарифма
логарифма 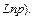
При 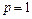 равенство (30.27) дает
равенство (30.27) дает 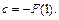
Поскольку 

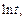 то получаем
то получаем
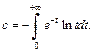
Известно, что
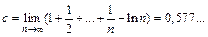
Число 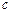 называют константой Эйлера.
называют константой Эйлера.
Таким образом, приходим к ответу
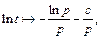
где 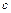 − константа Эйлера.
− константа Эйлера.
Пример 4. Найти оригинал для изображения 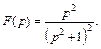
Решение. Запишем  в виде, который соответствует левой части равенства (30.24):
в виде, который соответствует левой части равенства (30.24):
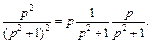
Известно, что (формулы (30.12), (30.13))
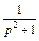

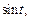
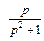

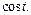
Тогда, согласно формуле Дюамеля (30.24), имеем
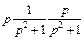

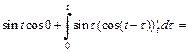
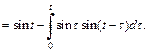
Вычислив последний интеграл
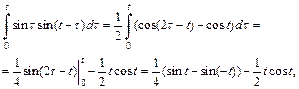
приходим к ответу
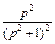

Date: 2015-09-02; view: 1637; Нарушение авторских прав