
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства оригинала и изображения
|
|
Оригиналы и изображения имеют следующие свойства.
1. Линейность изображения. Если 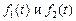 − оригиналы
− оригиналы 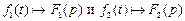 , то справедливо
, то справедливо
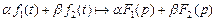 (30.4)
(30.4)
для любых констант 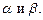
2. Свойство подобия. Если 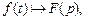 то для любого числа
то для любого числа 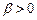 справедливо
справедливо
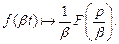 (30.5)
(30.5)
3. Смещение в области оригинала. Если 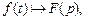 то для любого
то для любого 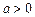 верны формулы
верны формулы
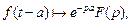 (30.6)
(30.6)
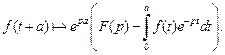 (30.7)
(30.7)
З а м е ч а н и е. Для функции f (t) оригинал f (t – а), при 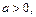 является функцией с аргументом, который запаздывает на величину а. Поэтому говорят, что формула (30.6) отражает свойство запаздывания. Аналогично формулу (30.7) рассматривают как свойство опережения.
является функцией с аргументом, который запаздывает на величину а. Поэтому говорят, что формула (30.6) отражает свойство запаздывания. Аналогично формулу (30.7) рассматривают как свойство опережения.
4. Смещение в области изображения. Если 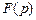

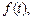 то для любого
то для любого 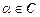 верна формула
верна формула
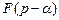

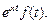 (30.8)
(30.8)
Сверткой двух функций 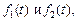 интегрируемых на бесконечном промежутке
интегрируемых на бесконечном промежутке 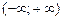 , называется функция
, называется функция 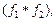 определяемая равенством
определяемая равенством
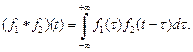 (30.9)
(30.9)
Если рассматриваются оригиналы f 1 (t) и f 2 (t), то 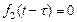 для
для 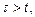 поэтому формула (30.9) для свертки оригиналов приобретает вид
поэтому формула (30.9) для свертки оригиналов приобретает вид
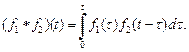 (30.10)
(30.10)
Теорема 2. Свертка двух оригиналов является оригиналом.
5. Изображение свертки. Если 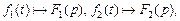 то верна формула
то верна формула
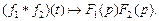 (30.11)
(30.11)
Пример 1. Найти изображение функции-оригинала f (t):
1) 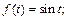 2)
2) 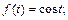 3)
3) 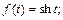 4)
4) 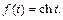
Решение. Для нахождения изображения оригинала 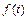 используем свойство линейности, формула (30.4), и найденное в примере 2, параграф 30.1, с. 7 данного пособия, изображение для
используем свойство линейности, формула (30.4), и найденное в примере 2, параграф 30.1, с. 7 данного пособия, изображение для 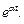
1) Согласно формуле 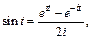 которую можно вывести, исходя из формул Эйлера
которую можно вывести, исходя из формул Эйлера 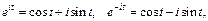 получаем
получаем
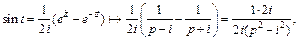
откуда 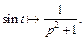 (30.12)
(30.12)
2) Согласно формуле 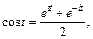 полученной аналогично, приходим к следующему изображению
полученной аналогично, приходим к следующему изображению
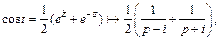
откуда 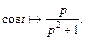 (30.13)
(30.13)
3) Используя определение функции sh t и свойство линейности изображения, получаем
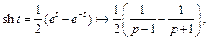
т. е. 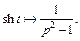 (30.14)
(30.14)
4) На основании определения функции сh t и свойства линейности изображения получаем
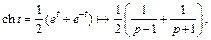
откуда 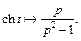 (30.15)
(30.15)
Пример 2. Найти изображение оригинала f (t):
1) 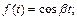 2)
2) 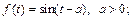
3) 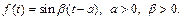
Решение. 1) Используя найденное ранее изображение cos t, формула (30.13), и свойство подобия (30.5), получаем
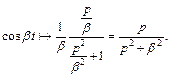 (30.16)
(30.16)
2) Применяя формулу (30.12) и свойство смещения в области оригинала, формула (30.6), получаем
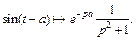
3) Аналогично тому, как найдено изображение для 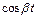 , найдем изображение для
, найдем изображение для 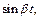 формула (30.12):
формула (30.12):
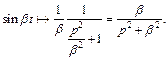 (30.17)
(30.17)
Применяя формулу (30.6), получаем
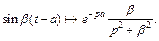
Пример 3. Найти изображение оригинала 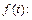
1) 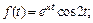 2)
2) 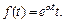
Решение. 1) Зная, что 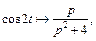 формула (30.16), и применяя свойство смещения в области изображения, формула (30.8), получаем
формула (30.16), и применяя свойство смещения в области изображения, формула (30.8), получаем
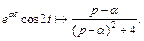
2) Зная, что 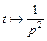 (см. пример 2, параграф 30.1, с. 7 данного пособия), аналогично предыдущему решению находим
(см. пример 2, параграф 30.1, с. 7 данного пособия), аналогично предыдущему решению находим
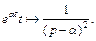
Пример 4. Найти изображение оригинала 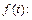
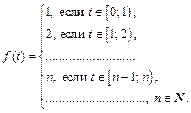
Решение. Функция 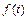 является ступенчатой (рис. 30.1).
является ступенчатой (рис. 30.1).
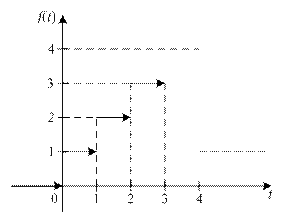
Рис. 30.1
Используя единичную функцию (функцию Хевисайда) 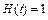 (см. пример 2, параграфа 30.1, с. 7 данного пособия), функцию
(см. пример 2, параграфа 30.1, с. 7 данного пособия), функцию 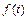 можно записать в виде
можно записать в виде
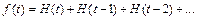
Как было показано в примере 2, параграф 30.1, с. 7 данного пособия, 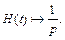 Тогда согласно свойству линейности изображения, формула (30.4), и в соответствии с формулой (30.6) получаем
Тогда согласно свойству линейности изображения, формула (30.4), и в соответствии с формулой (30.6) получаем
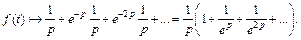
По формуле суммы элементов бесконечно убывающей геометрической прогрессии приходим к ответу
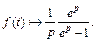
Пример 5. Найти оригинал 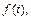 если известно, что соответствующее изображение
если известно, что соответствующее изображение  есть:
есть:
1) 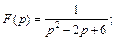 2)
2) 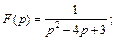
3) 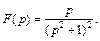
Решение. 1) Преобразуем выражение для  следующим образом:
следующим образом:
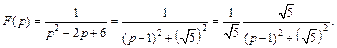
Используя формулы (30.8) и (30.17), получаем
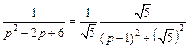

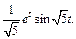
Откуда 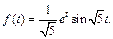
2 ) 1-й способ. Как и в предыдущем примере, находим
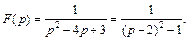
Применяя формулы (30.8) и (30.14), получаем
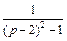

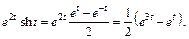
Таким образом,
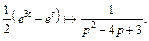
2-й способ. Преобразуем  следующим образом:
следующим образом:
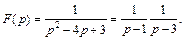
Так как  (см. пример 2, параграф 30.1, с. 7 данного пособия), то
(см. пример 2, параграф 30.1, с. 7 данного пособия), то
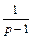


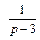


Согласно формуле (30.11), получаем
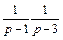

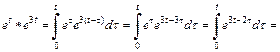
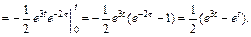
3) Запишем изображение в виде произведения:
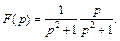
Используя формулы (30.12) и (30.13), имеем
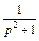

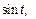
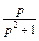

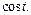
Тогда согласно свойству умножения изображений, формула (30.11), получаем
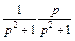

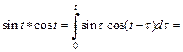
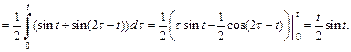
Таким образом, приходим к соотношению
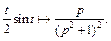 (30.18)
(30.18)
Date: 2015-09-02; view: 3687; Нарушение авторских прав