
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Операционное исчисление
|
|
Основные понятия операционного исчисления
Функция f (t) действительной переменной 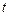 называется оригиналом (функцией-оригиналом), если она удовлетворяет следующим условиям:
называется оригиналом (функцией-оригиналом), если она удовлетворяет следующим условиям:
1) f (t) является кусочно-непрерывной, интегрируемой на любом конечном интервале оси 
2) существуют константы 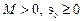 такие, что
такие, что  (30.1)
(30.1)
3) 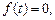

Константу  называют показателем роста функции f (t).
называют показателем роста функции f (t).
Простейшим примером функции-оригинала является единичная функция (функция Хевисайда):

Если некоторая функция f (t) удовлетворяет первым двум условиям функции-оригинала, а третьему условию она не удовлетворяет, то операция умножения ее на функцию Н (t) приводит к оригиналу Н (t) f (t):

Вместо Н (t) f (t) будем писать просто f (t) и всегда понимать, что f (t) = 0 при любом 
Изображением функции f (t) называется функция F (р) комплексной переменной  которая определяется равенством
которая определяется равенством
 (30.2)
(30.2)
Интеграл, входящий в равенство (30.2), называется преобразованием Лапласа, поэтому функцию F (р) называют еще изображением по Лапласу функции f (t).
Словесное выражение «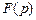 является изображением для оригинала
является изображением для оригинала  » записывают так:
» записывают так:
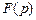


выражение же « является оригиналом для
является оригиналом для 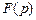 » записывается так:
» записывается так:
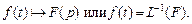
Теорема 1. Для любого оригинала  соответствующее изображение
соответствующее изображение 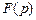 является аналитической функцией в полуплоскости
является аналитической функцией в полуплоскости 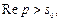 где
где 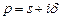 ,
,  − показатель роста функции
− показатель роста функции 
Если точка  стремится к бесконечности так, что
стремится к бесконечности так, что  неограниченно возрастает, то
неограниченно возрастает, то
 (30.3)
(30.3)
Замечание. Не всякая функция может быть изображением некоторого оригинала.
Пример 1. Выяснить, является ли оригиналом функция 
1) 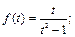 2)
2) 
Решение. 1) В точке 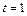 функция
функция  имеет разрыв второго рода, т. е. в этой точке она является бесконечно большой функцией. Но тогда условие (30.1) не выполняется, следовательно, функция
имеет разрыв второго рода, т. е. в этой точке она является бесконечно большой функцией. Но тогда условие (30.1) не выполняется, следовательно, функция 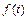 не является оригиналом.
не является оригиналом.
2) Для степенной функции с произвольным натуральным показателем n имеем

в чем можно убедиться, например, применив n раз правило Лопиталя. Поэтому, существует константа М такая, что

Это приводит к заключению, что  является оригиналом.
является оригиналом.
Пример 2. Найти изображение данного оригинала:
1) 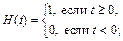 2)
2)  3)
3) 
Решение. 1) Функция 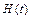 задана двумя значениями, одно из которых является нулевым при всех
задана двумя значениями, одно из которых является нулевым при всех 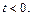 Согласно сказанному выше, эту функцию будем задавать в виде
Согласно сказанному выше, эту функцию будем задавать в виде  Используя формулу (30.2), получаем
Используя формулу (30.2), получаем
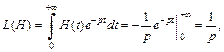
где  т. е. для единичной функции
т. е. для единичной функции 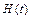
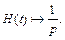
2) Используя формулу (30.2), получаем

если  т. е.
т. е.  то используя формулу (30.2), имеем
то используя формулу (30.2), имеем

3) Используя формулу (30.2) и метод интегрирования по частям, получаем
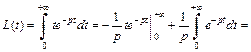
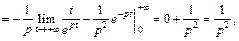
где  Таким образом
Таким образом 
Date: 2015-09-02; view: 1393; Нарушение авторских прав