Знакоопределенные квадратичные формы

Действительная квадратичная форма f (x₁,x₂…,x_n) называется положитель­но-определенной, если она приводится к нормальному виду, состоящему из п по­ложительных квадратов: f (x₁,x₂…,x_n) ~ φ (y₁, y₂….y_n), где (1.9), т. е. если ранг и положительный индекс инерции равны числу неизвестных.
Систему значений x₁,x₂…,x_n назовем нулевой, если x₁= х₂ =... = x_n =0, и ненулевой, если хотя бы одно из них отлично от нуля.
Теорема 6. Действительная квадратичная форма f (x₁,x₂…,x_n) является положительно-определенной тогда и только тогда, когда она принимает положительные значения при любой ненулевой системе значений переменных x₁, x₂…,x_n. Пусть дана квадратичная форма f (x₁,x₂…,x_n) с матрицейА = (а_у). Глав­ными минорами квадратичной формы f называются миноры, т. е. миноры порядка 1, 2,..., п матрицы А, расположенные в левом верхнем углу; последний из них совпадает с определителем матрицы.
Теорема 7. Квадратичная форма f (x₁,x₂…,x_n) с действительной
матрицей является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны.
Действительная квадратичная форма называется отрицательно-определенной, ес­ли она является невырожденной и приводится к нормальному виду, содержащему только отрицательные квадраты всех переменных; эту форму можно привести к виду:φ (y₁, y₂….y_n)= -y²₁ – y²₂ -…- y²_n (1.10).
Теорема 8. Квадратичная форма является отрицательно-определенной тогда и только тогда, когда ее главные миноры четного порядка положительны, а нечетного - отрицательны.
Положительно-определенные и отрицательно-определенные квадратичные формы называются знакоопределенными квадратичными формами.
Вырожденные квадратичные формы, нормальный вид которых состоит из квадратов одного знака, называются полуопределенными.Неопределенными называются квадратичные формы, нормальный вид которых содержит как положительные, так и отрицательные квадраты переменных.
Пример. Доказать, что квадратичная форма f (x₁, x₂, x₃)
= 6x²₁+ 5х²₂ + 7х²₃ - 4х₁х₂ + 4х₁x₃ положительно-определенная.

Запишем матрицу A этой квадратичной формы и определитель матрицы А:
Так как главные миноры матрицы a₁₁=6, все положительны, то данная квадратичная форма является положительно-определенной.
32. В качестве примера математической модели экономического процесса, приводящей к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли). [1]

Рассмотрим n стран S₁,S₂,...S_n, национальный доход каждой из которых равен соответственно x₁,x₂,...x_n. Обозначим коэффициентами a_IJ часть национального дохода, которую страна S_J тратит на покупку товаров у страны S_I. Считаем, что весь национальный доход тратиться на закупку товаров либо внутри страны, либо у других стран.

Тогда,приняв национальный доход за единицу, для частей этого дохода имеющихся у страны j имеем равенство

(j=1,2...n)

Рассмотрим матрицу

- структурную матрицу торговли.

Сумма элементов любого столбца матрицы А равна 1. Для любой страны S_I (i=1,2,...,n) выручка от внутренней и внешней торговли составит:

p_i=a_i1x₁+a_i2x₂+...+a_inx_n.

Для наличия сбалансированной торговли необходима бездифицитность торговли каждой страны S_i, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода [1]:

p_i³x_i (i=1,2,...,n),

а значит получаем систему неравенств

Сложив все неравенства системы (2), получим

x₁(a₁₁+a₂₁+..+a_n1)+x₂(a₁₂+a₂₂+..+a_n2)+..+x_n(a_1n+a_2n+..+a_nn)x₁+x₂+...+x_n.

Выражения в скобках равны единице, а поэтому мы приходим к неравенству

x₁ + x₂ +...+x_n x₁ + x₂ +...+ x_n,

которое выполняется только в случае равенства, а поэтому имеем систему

Если вектор - вектор национальных доходов стран, то уравнение (3) можно записать в виде

Ax= т.е. задача свелась к отысканию собственного вектора матрицы А, отвечающего собственному значению l=1.

33. Определение. Уравнением линии называется соотношение y = f(x) между координатами точек, составляющих эту линию

Отметим, что уравнение линии может быть выражено параметрическим способом, то есть каждая координата каждой точки выражается через некоторый независимый параметр t. Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.

Уравнение прямой на плоскости.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно, т.е. А² + В² ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.

В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

- C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат

- А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох

- В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу

- В = С = 0, А ¹ 0 – прямая совпадает с осью Оу

- А = С = 0, В ¹ 0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Расстояние от точки до прямой.

Теорема. Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

.

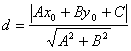Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М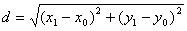₁:

(1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

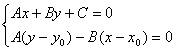
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим:

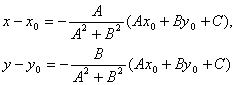
Подставляя эти выражения в уравнение (1), находим:

.

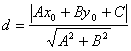Теорема доказана.

Date: 2015-08-24; view: 571; Нарушение авторских прав