Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Простейшие свойства
|
|
1. Векторное пространство является абелевой группой по сложению.
2. Нейтральный элемент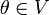 
является единственным, что вытекает из групповых свойств.
3. 
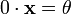для любого 
.
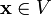4. Для любого 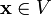противоположный элемент 
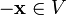является единственным, что вытекает из групповых свойств.
5. 
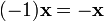для любого .
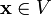6. 
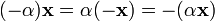для любых 
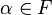и .
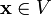7. 
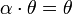для любого .
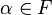22. Переход к новому базису. Пусть в пространстве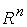 
имеется два базиса: 
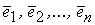и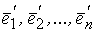 
.
Первый условимся называть старым базисом, второй – новым. Каждый из векторов нового базиса, по Теореме 5.1, можно линейно выразить через векторы старого базиса:
(5.1)
Новые базисные векторы получаются из старых с помощью матрицы
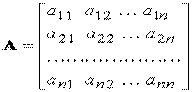
При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица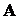 
называется матрицей перехода от базиса 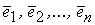к базису .
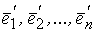Определитель матрицы 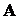не равен нулю, так как в противном случае ее столбцы, а следовательно и векторы 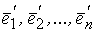, были бы линейно зависимы.
Обратно, если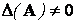 
, то столбцы матрицы линейно независимы, и следовательно векторы 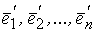, получающиеся из базисных векторов 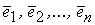с помощью матрицы 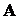, линейно независимы и значит образуют некоторый базис. Таким образом, матрицей перехода может служить любая квадратная матрица порядка n с отличным от нуля определителем.
Date: 2015-08-24; view: 394; Нарушение авторских прав