Связь между матрицами одного и того же линейного оператора в разных базисах

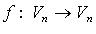Если в базисе линейный оператор имеет матрицу A, в базисе 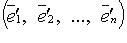- матрицу B, а S - матрица перехода от первого базиса ко второму, то

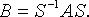
Произведение и сумма линейных операторов

Если f и g - линейные операторы пространства 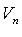с матрицами A и B в базисе 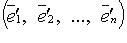, то операторы произведения 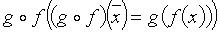и суммы 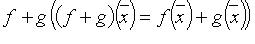- линейные и имеют в том же базисе матрицы BA и A + B соответственно.

Оператор, обратный данному линейному оператору

Линейный оператор 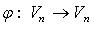называется обратным линейному оператору 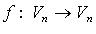, если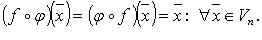

Обозначение: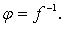

Для существования 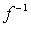необходимо и достаточно, чтобы f был невырожденным оператором. Если A - матрица оператора f в некотором базисе, то оператор 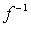в том же базисе имеет матрицу .

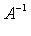Ядро и область значений линейного оператора

Ядро оператора: 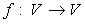- множество, обозначаемое Ker f:

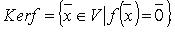
Область значений (образ) оператора 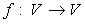- множество, обозначаемое Im f:

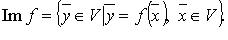
Множества Ker f и Im f являются подпространствами пространства V.

Ранг оператора 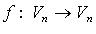(обозначение: dim Im f) - ранг матрицы A линейного оператора f,

dim Im f = rank A.

Дефектом оператора 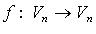называют dim Ker f,

dim Im f + dim Ker f = n.

27. Собственные значения и собственные векторы линейного оператора

Пусть 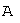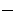линейный оператор, действующий в линейном пространстве.

Число 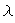называется собственным значением, а ненулевой вектор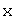 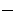соответствующим собственным вектором линейного оператора 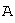, если они связаны между собой соотношением .

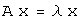Пусть 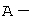матрица оператора в некотором базисе.

Собственные значения оператора и соответствующие им собственные векторы связаны соотношением 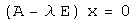, где 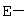единичная матрица, а 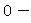нулевой элемент пространства 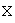. Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы 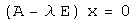, которое существует тогда и только тогда, когда 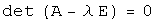. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения 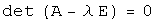, а собственные векторы -- как решения соответствующих однородных систем.

Уравнение 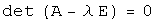называется характеристическим уравнением оператора, а многочлен 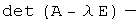характеристическим многочленом оператора.

Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:

характеристический многочлен оператора, действующего в n-мерном линейном пространстве является многочленом n-й степени относительно ;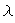

линейный оператор, действующий в n-мерном линейном пространстве имеет не более 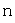различных собственных значений;

собственные векторы, отвечающие различным собственным значениям, линейно независимы;

если линейный оператор, действующий в n-мерном линейном пространстве 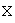, имеет 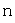различных собственных значений, то собственные векторы оператора образуют базис в пространстве 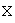; этот базис называют собственным базисом оператора;

матрица оператора в базисе из его собственных векторов имеет диагональную форму с собственными значениями на диагонали.

28. Приведение матрицы линейного оператора к диагональной форме

Таким образом можно описать алгоритм приведения матрицы линейного оператора к диагональной форме.

Он состоит в следующем:

· записываем матрицу оператора A в исходном базисе;

· записываем характеристическое уравнение и вычисляем его корни;

· находим собственный базис оператора (если он существует);

· записываем матрицу C, столбцами которой являются координаты собственных векторов (векторов собственного базиса);

· по формуле C^-1AC находим диагональную форму матриц оператора — матрицу оператора в собственном базисе.

Date: 2015-08-24; view: 2135; Нарушение авторских прав