Понятие размерности векторного пространства и базиса

Понятия размерности и базиса векторного пространства напрямую связаны с понятием линейно независимой системы векторов, так что рекомендуем при необходимости обращаться к статье линейная зависимость системы векторов, свойства линейной зависимости и независимости.

Определение.

Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Определение.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

Приведем некоторые рассуждения, основываясь на этих определениях.

Рассмотрим пространство n-мерных векторов.

Покажем, что размерность этого пространства равна n.

Возьмем систему из n единичных векторов вида

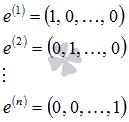
Примем эти векторы в качестве строк матрицы А. В этом случае матрица А будет единичной матрицей размерности n на n. Ранг этой матрицы равен n (при необходимости смотрите статью ранг матрицы: определение, методы нахождения). Следовательно, система векторов 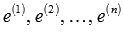линейно независима, причем к этой системе нельзя добавить ни одного вектора, не нарушив ее линейной независимости. Так как число векторов в системе 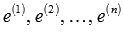равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы 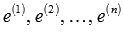являются базисом этого пространства.

Из последнего утверждения и определения базиса можно сделать вывод, что любая системаn-мерных векторов, число векторов в которой меньше n, не является базисом.

Теперь переставим местами первый и второй вектор системы 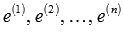. Легко показать, что полученная система векторов 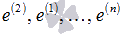также является базисом n-мерного векторного пространства. Составим матрицу, приняв ее строками векторы этой системы. Эта матрица может быть получена из единичной матрицы перестановкой местами первой и второй строк, следовательно, ее ранг будет равен n. Таким образом, система из n векторов 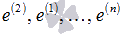линейно независима и является базисом n-мерного векторного пространства.

Если переставить местами другие векторы системы 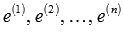, то получим еще один базис.

Если взять линейно независимую систему не единичных векторов, то она также является базисом n-мерного векторного пространства.

Таким образом, векторное пространство размерности n имеет столько базисов, сколько существует линейно независимых систем из n n-мерных векторов.

Если говорить о двумерном векторном пространстве (то есть, о плоскости), то ее базисом являются два любых не коллинеарных вектора. Базисом трехмерного пространства являются три любых некомпланарных вектора.

Рассмотрим несколько примеров.

Пример.

Являются ли векторы 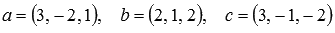базисом трехмерного векторного пространства?

Решение.

Исследуем эту систему векторов на линейную зависимость. Для этого составим матрицу, строками которой будут координаты векторов, и найдем ее ранг:

Таким образом, векторы a, b и c линейно независимы и их количество равно размерности векторного пространства, следовательно, они являются базисом этого пространства.

Ответ:

да, являются.

Пример.

Может ли система векторов быть базисом векторного пространства?

Решение.

Эта система векторов линейно зависима, так как максимальное число линейно независимых трехмерных векторов равно трем. Следовательно, эта система векторов не может быть базисом трехмерного векторного пространства (хотя подсистема 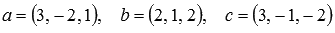исходной системы векторов является базисом).

Ответ:

нет, не может.

Пример.

Убедитесь, что векторы

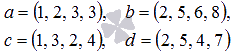
могут быть базисом четырехмерного векторного пространства.

Решение.

Составим матрицу, приняв ее строками исходные векторы:

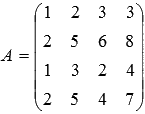
Найдем ранг матрицы методом Гаусса:

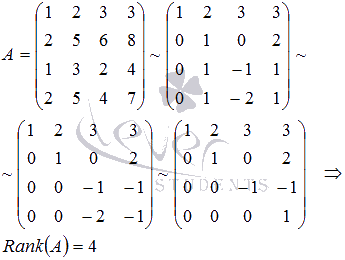
Таким образом, система векторов a, b, c, d линейно независима и их количество равно размерности векторного пространства, следовательно, a, b, c, d являются его базисом.

Ответ:

исходные векторы действительно являются базисом четырехмерного пространства.

Пример.

Составляют ли векторы 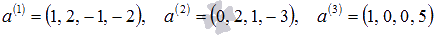базис векторного пространства размерности 4?

Решение.

Даже если исходная система векторов линейно независима, количество векторов в ней недостаточно для того, чтобы быть базисом четырехмерного пространства (базис такого пространства состоит из 4 векторов).

Ответ:

нет, не составляет.

21. Линейное, или векторное пространство 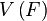над полем 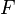— это упорядоченная четвёрка 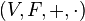, где

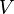— непустое множество элементов произвольной природы, которые называются векторами;

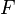— (алгебраическое) поле, элементы которого называются скалярами;

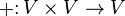— операция сложения векторов, сопоставляющая каждой паре элементов 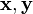множества 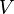единственный элемент множества 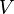, обозначаемый ;

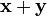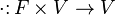— операция умножения векторов на скаляры, сопоставляющая каждому элементу 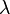поля 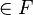и каждому элементу 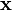множества 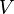единственный элемент множества 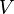, обозначаемый ;

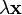причём, заданные операции удовлетворяют следующим аксиомам — аксиомам линейного (векторного) пространства:

1. 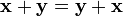, для любых 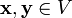(коммутативность сложения);

2. , для любых 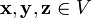(ассоциативность сложения);

3. существует такой элемент 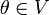, что 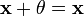для любого 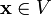(существование нейтрального элемента относительно сложения), в частности 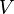не пусто;

4. для любого 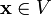существует такой элемент 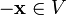, что 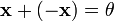(существование противоположного элемента относительно сложения).

5. 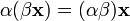(ассоциативность умножения на скаляр);

6. 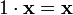(унитарность: умножение на нейтральный (по умножению) элемент поля F сохраняет вектор).

7. 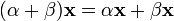(дистрибутивность умножения на вектор относительно сложения скаляров);

8. 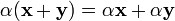(дистрибутивность умножения на скаляр относительно сложения векторов).

Таким образом, операция сложения задаёт на множестве 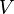структуру (аддитивной) абелевой группы.

Векторные пространства, заданные на одном и том же множестве элементов, но над различными полями, будут различными векторными пространствами.

В качестве дополнительной (девятой) аксиомы векторного пространства иногда используют следующую: размерность пространства равна некоторому натуральному числу (если существует максимальная линейно независимая система векторов данного пространства или, что тоже самое, существует конечная порождающая система векторов данного пространства), и тогда такое пространство называют конечномерным, или говорят, что пространство бесконечномерное (если не существует конечной порождающей системы векторов данного пространства). В соответствии с этим, теория линейных (векторных) пространств разделяется на две различные части: теорию конечномерных пространств, в которой существенным оказывается алгебраический аспект, и теорию бесконечномерных пространств, где главным оказывается аспект анализа — вопрос о разложимости данного элемента по заданной бесконечной системе функций.

Date: 2015-08-24; view: 786; Нарушение авторских прав