
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Фундаментальная система решений
|
|

| Теорема (о ФСР). Пусть ранг основной матрицы 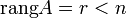 , где , где 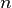 — число переменных системы (1), тогда:
· ФСР (1) существует: — число переменных системы (1), тогда:
· ФСР (1) существует: 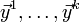 ;
· она состоит из ;
· она состоит из 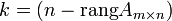 векторов;
· общее решение системы имеет вид векторов;
· общее решение системы имеет вид 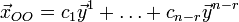 .
Замечание: Если .
Замечание: Если  , то ФСР не существует. , то ФСР не существует.
|
Пример:
Решим систему
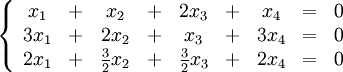
Перепишем её в матричном виде:
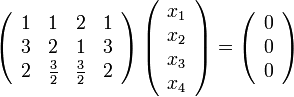
Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:
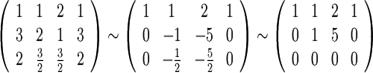
Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует 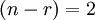 линейно независимых решения системы.
линейно независимых решения системы.
Перепишем полученную систему в виде уравнений:
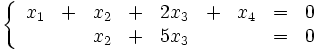
Возьмём 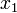 и
и  в качестве главных переменных. Тогда:
в качестве главных переменных. Тогда:
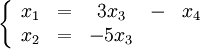
Подставим по очереди единицы в качестве одной из свободных переменных: 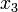 и
и 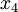 .
.

Тогда общее решение рассматриваемой системы может быть записано так:
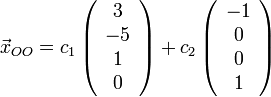 ,
,
а вектора 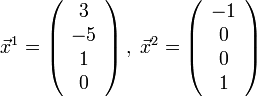 составляют фундаментальную систему решений.
составляют фундаментальную систему решений.
13. Модель Леонтьева. В 1930-е годы Василий Леонтьев применил метод анализа межотраслевых связей с привлечением аппарата линейной алгебры для исследования экономики США. Метод стал известен под названием «затраты — выпуск». Во время Второй мировой войны, разработанная Леонтьевым матрица «затраты — выпуск» для экономики Германии служила для выбора целей ВВС США[2]. Аналогичный баланс для СССР, разработанный Леонтьевым, использовался властями США для принятия решения об объёмах и структуре Ленд-лиза.
Межотраслевой баланс (МОБ, метод «затраты-выпуск») — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. Межотраслевой баланс составляется в денежной и натуральной формах.
Межотраслевой баланс представлен в виде системы линейных уравнений. Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого продукта и структуру его распределения в экономике. По столбцам отражается стоимостный состав валового выпуска отраслей экономики по элементам промежуточного потребления и добавленной стоимости. По строкам отражаются направления использования ресурсов каждой отрасли.
В Модели МОБ выделяются четыре квадранта. В первом отражается промежуточное потребление и система производственных связей, во втором — структура конечного использования ВВП, в третьем — стоимостная структура ВВП, а в четвёртом — перераспределение национального дохода.
Пример расчета межотраслевого баланса
Рассмотрим 2 отрасли промышленности: производство угля и стали. Уголь требуется для производства стали, а некоторое количество стали — в виде инструментов — нужно для добычи угля. Предположим, что условия таковы: для производства 1 т стали нужно 3 т угля, а для 1 т угля — 0,1 т стали.
| Отрасль | Уголь | Сталь |
| Уголь | ||
| Сталь | 0.1 |
Мы хотим, чтобы чистый выпуск угольной промышленности был 200 000 тонн угля, а чёрной металлургии — 50 000 тонн стали. Если каждая из них будет производить лишь 200000 и 50000 тонн, то часть продукции будет использоваться в другой отрасли.
Для производства 50000 тонн стали требуется 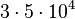 = 150 000 тонн угля, а для производства 200000 тонн угля нужно
= 150 000 тонн угля, а для производства 200000 тонн угля нужно 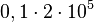 = 20 000 тонн стали. Чистый выход будет равен:
= 20 000 тонн стали. Чистый выход будет равен: 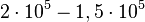 = 50 000 тонн угля и
= 50 000 тонн угля и 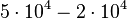 = 30 000 тонн стали.
= 30 000 тонн стали.
Нужно дополнительно производить уголь и сталь, чтобы использовать их в другой отрасли. Обозначим 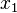 — количество угля,
— количество угля, 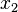 — количество стали. Валовый выпуск каждой продукции найдем из системы уравнений:
— количество стали. Валовый выпуск каждой продукции найдем из системы уравнений:
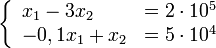
Решение: 500 000 т угля и 100 000 т стали. Для систематического решения задач расчета межотраслевого баланса находят, сколько угля и стали требуется для выпуска 1 т каждого продукта.
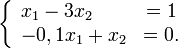
 и
и 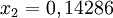 . Чтобы найти, сколько угля и стали нужно для чистого выпуска
. Чтобы найти, сколько угля и стали нужно для чистого выпуска 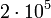 т угля, нужно умножить эти числа на
т угля, нужно умножить эти числа на 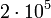 . Получим:
. Получим: 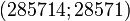 .
.
Аналогично составляем уравнения для получения количества угля и стали для выпуска 1 т стали:
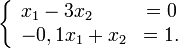
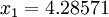 и
и 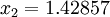 . Для чистого выпуска
. Для чистого выпуска 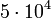 т стали нужно: (214286; 71429).
т стали нужно: (214286; 71429).
Валовый выпуск для производства 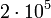 тонн угля и
тонн угля и 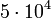 тонн стали:
тонн стали: 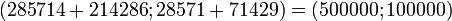
14Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв). Числа (символы), определяющие положение точки (тела) на прямой, плоскости, в пространстве, на поверхности и так далее, называются её координатами. В зависимости от целей и характера исследования выбирают различные системы координат.
Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.
Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.
Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:
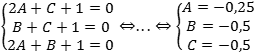
Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.
Ответ: − 0,25x − 0,5y − 0,5z + 1 = 0
15.Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр[1]. Введённые операции подчинены восьми аксиомам.[⇨] Скаляром же может являться элемент вещественного, комплексногоили любого другого поля чисел. Частным случаем векторов подобного пространства являются обычные евклидовы вектора, которые используются, к примеру, для демонстрациифизических сил. При этом следует отметить, что вектор как элемент векторного пространства не обязательно должен быть представлен в качестве направленного отрезка. Обобщение понятия «вектор» до элемента векторного пространства любой природы не только не вызывает смешения терминов, но и позволяет уяснить или даже предвидеть ряд результатов, справедливых для пространств произвольной природы.
Date: 2015-08-24; view: 637; Нарушение авторских прав