Свойства векторного произведения

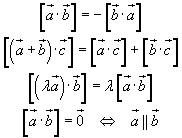
Смешанное произведение векторов (векторно-скалярное произведение)

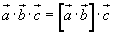
17 Базисом в пространстве Rⁿ называется любая система из n -линейно независимых векторов. Каждый вектор из Rⁿ, не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.
Пусть 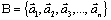– базис пространства Rⁿ и 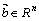. Тогда найдутся такие числа λ₁, λ₂, …, λ_n, что .
Коэффициенты разложения λ₁, λ₂, …, λ_n, называются координатами вектора 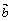в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.
Пример. Доказать, что векторы 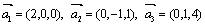образуют базис в R³.
Решение. Покажем, что равенство 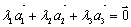возможно только при λ₁ = λ₂ = λ₃ =0:

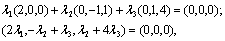
или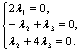
Решив систему, получим λ₁=0, λ₂=0, λ₃=0. Так как все λ _i =0 (i =1,2,3), то 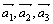- линейно независимы. Они могут составить базис в R³.
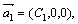
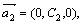
Очевидно, любой новый набор из векторов 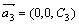может тоже быть взятым в качестве базиса в R³. Итак, базис может быть выбран неединственным образом.
Пример. Разложить вектор 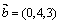по базису .
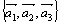Решение. 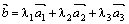. Подставим координаты всех векторов и выполним действия над ними:

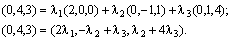
Приравняв координаты, получим систему уравнений:

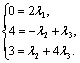
Решим ее: .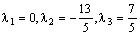
Таким образом, получим разложение: .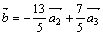
В базисе 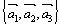вектор 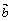имеет координаты .
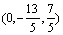Замечание. В каждом n -мерном векторном пространстве можно выбрать бесчисленное множество различных базисов. В различных базисах один и тот же вектор имеет различные координаты, но единственные в выбранном базисе.

18. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через их координаты. Приложения.

Определение 2.7.1. Углом ϕ между векторами a, b называется угол между векторами, равными данным и имеющими общее начало. Если не указано, от какого вектора и в каком направлении угол отсчитывается, то углом между векторами считается тот из углов, который не превосходит π. Если угол прямой, то векторы называются ортогональными.

Определение 2.7.2.Скалярным произведением векторов a, b называется число a⋅b или (a,b), равное произведению длин векторов на косинус угла между ними:

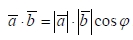
Свойства скалярного произведения:
1. a⋅b=b⋅a;
2. a⋅b=0 тогда и только тогда, когда векторы ортогональны;
3. Для любых чисел α,β и векторов a,b,c имеет место соотношение: (αa+βb)⋅c=α(a⋅c)+β(b⋅c) (линейность скалярного произведения);
4. a⋅a=|a|2.
Теорема 2.7.1. Если базис ортонормированный, то скалярное произведение векторов
выражается через их компоненты a ={a1;a2;a3}, b = {b1;b2;b3} по формуле
a⋅b =a1b1+a2b2+a3b3.
Следствия:
1. Модуль вектора вычисляется по формуле

2. Косинус угла между векторами вычисляется по формуле

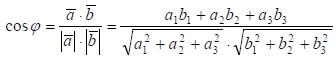
3. Если векторы a и b ортогональны, то их координаты связаны соотношением

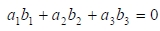
Механическое приложение скалярного произведения. Работа силы F по
перемещению точки равна скалярному произведению A = F ⋅ r, где r – вектор перемещения.

19. Вектором размерности n называется упорядоченный набор из n действительных чисел. Будем записывать вектор в ви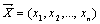де , где 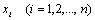- координаты вектора. Размерность вектора определяется числом его координат и является его отличительной характеристикой. Векторы равны, если они одной размерно-сти и имеют равные соответствующие координаты: (2,3,5) = (2,3,5). Нуль-вектор 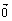= (0,0,…,0) не следует путать с числом нуль.
Определение. Множество всех векторов размерности n называется арифметическим n -мерным векторным пространством и обозначается Rⁿ.
Экономические величины являются многофакторными (многомерными), и n -мерные векторы служат удобной формой их представления. Например, некоторый набор товаров различных сортов можно охарактеризовать вектором 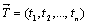, а соответствующие цены – вектором .

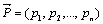2. Действия над n -мерными векторами

Пусть даны векторы 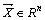и .
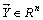Определение. Суммой векторов 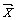и 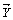называется вектор 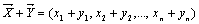, т.е. при сложении векторов их соответствующие координаты складываются: (2, –4) + (–2, 4) = (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2, –6,5).
Определение. Произведением вектора 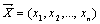на число 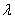называется вектор 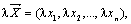т.е. при умножении вектора на число каждая его координата умножается на это число.
Можно проверить, что введенные таким образом операции над векторами удовлетворяют всем свойствам операций в линейном пространстве. Следовательно, арифметическое n -мерное пространство R ⁿ является частным случаем введенного ранее линейного пространства.
Определение. Скалярным произведением двух векторов 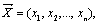и называется число, равное сумме произведений соответствующих координат векторов: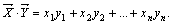
Пример: Пусть 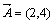и .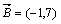
Тогда .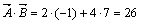
Скалярное произведение обладает следующими свойствами:
1. 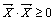, причем 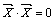, только при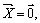
2. ,
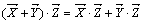3. ,
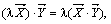4. .
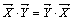Определение. Два вектора называются ортогональными, если их скалярное произведение равно 0, т.е. .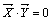
Пример. Пусть 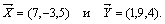Тогда 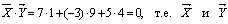ортогональны.
Определение. Линейное пространство с введенным скалярным произведением называется евклидовым n -мерным пространством.
Примеры:
1. Множество трехмерных векторов R³.
2. Множество двумерных векторов R².
3. Множество R¹ = R – множество действительных чисел.

Date: 2015-08-24; view: 724; Нарушение авторских прав