Основні властивості криволінійного інтеграла першого роду

а) криволінійний інтеграл першого роду не залежить від напрямку шляху інтегрування: ;

б) ;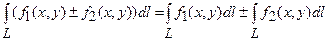

в) , де k = const;

г) якщо крива 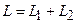, то

;

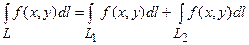Криволінійний інтеграл першого роду при обчисленні зводяться до визначеного інтегралу:

а) якщо крива 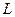задана рівнянням 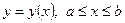, то

;

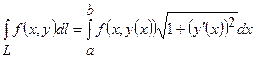б) якщо крива 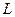задана параметричним рівнянням 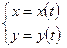, , 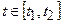то ;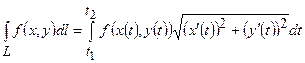

в) у випадку просторової кривої, яка має рівняння

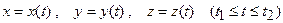матимемо

;

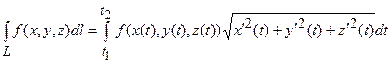Криволінійний інтеграл першого роду застосовують для знаходження:

а) обчислення довжини кривої 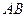здійснюється за формулою: ;

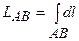б) якщо циліндрична поверхня, твірні якої паралельні осі 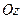, опирається на криву 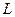в площині , а зверху обмежена поверхнею , то площа такої циліндричної поверхні обчислюється за формулою: ;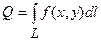

в) маса матеріальної кривої обчислюється за формулою: 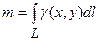, де – лінійна густина;

г) координати 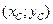центра маси кривої 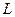знаходяться за формулами:

,

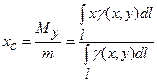
де 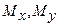– статичні моменти кривої відносно осей 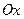і 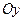. У випадку, коли розглядається однорідна матеріальна крива, слід покласти ;

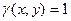д) моменти інерції 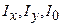кривої 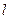відносно осей і

початку координат обчислюються за формулами:

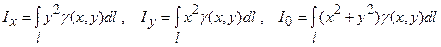
Задача 27. Обчислити криволінійний інтеграл першого роду 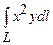, де 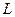– частина кола 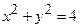, розміщена в першій чверті .

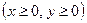Розв’язання: Запишемо рівняння кола у вигляді 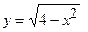, . Знайдемо : ,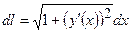

.

Тоді .

Криволінійний інтеграл другого роду (по координатах) це , де функції 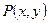, 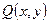визначені і обмежені на кривій .

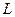Основні властивості криволінійного інтеграла другого роду:

а) криволінійний інтеграл другого роду змінює свій знак на протилежний при зміні напрямку шляху інтегрування

;

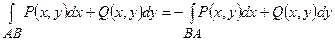б) ;

Інші властивості аналогічні властивостям інтеграла першого роду.

Криволінійний інтеграл другого роду при обчисленні зводяться до визначеного інтегралу:

а) якщо крива 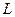задана рівнянням 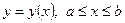, то

;

б) якщо крива 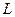задана параметричним рівнянням 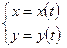, , 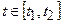то

;

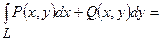
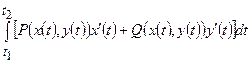в) криволінійний інтеграл другого роду залежить від шляху інтегрування:

;

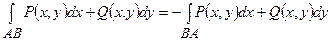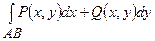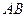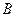Якщо , то значення інтеграла не залежить від форми кривої , яка сполучає точки та і 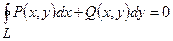, а вираз 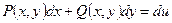– повний диференціал функції 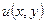, яку можна відновити використовуючи формули:

або

,

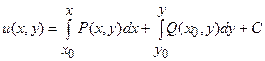де 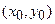довільна фіксована точка, в якій визначені функції , .

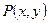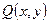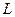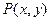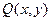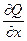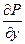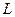Якщо – замкнений контур, який обмежує область і функції і неперервні, разом із своїми частинними похідними 1-го порядку: і в замкненій області включаючи межу , то справедлива формула Гріна:

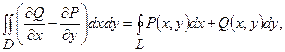
де обхід контуру 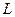вибирається таким, щоб область залишалась зліва.

Криволінійний інтеграл другого роду застосовують для знаходження:

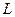а) площі плоскої фігури , обмеженої кривою , за формулою: ;

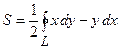б) роботи сили 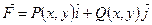при переміщенні матеріальної точки вздовж кривої : .

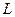Задача 28. Обчислити криволінійний інтеграл другого роду 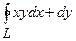, де 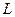– замкнений контур, утворений лініями .

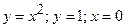Розв’язання: Для замкненого контуру існує лише два напрями

обходу: проти стрілки годинника (додатна орієнтація контуру) та за стрілкою годинника (від¢ємна орієнтація контуру). При додатній орієнтації контуру він завжди залишається зліва при його обході.

Маємо:

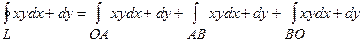
1) рівняння : 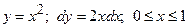, тоді

;

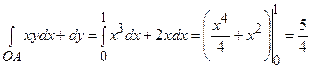2) рівняння 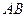: , 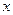змінюється від 1 до 0, тоді

;

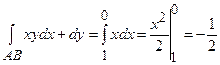3) рівняння : , 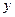змінюється від 1 до 0, тоді

;

Тоді

Задача 29. Впевнитись, що вираз

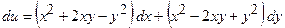є повним диференціалом деякої функції і знайти цю функцію.

Розв’язання: З даного виразу випливає 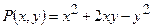, . Знайдемо частинні похідні , .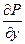

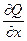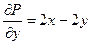, . Оскільки , то вираз дійсно є повним диференціалом деякої функції 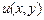. Знайдемо цю функцію за допомогою формули

.

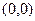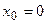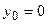В якості точки можна взяти точку : , . Тоді

.

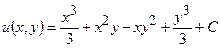
Date: 2015-08-24; view: 466; Нарушение авторских прав