Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Параметр эффективного трения Г. Конформационная динамика RyR-канала
|
|
Коэффициент эффективного трения Г, входящий в уравнение Ланжевена (2.7), влияет на характер изменения конформационной координаты Q со временем. Приведенное уравнение (М =1) изменения конформационной координаты при отсутствии тепловых возмущений (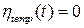
) может быть записано в терминах затухающего гармонического осциллятора:
, (3.4)
где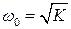 
– характерная частота колебаний гармонического осциллятора.
При малом трении (Г<2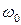 
) общее решение может быть представлено в виде [118]:
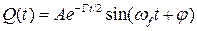, (3.5)
где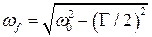 
– частота свободных колебаний; А, φ – амплитуда и фаза затухающих колебаний, соответственно.
При Г=2 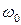затухание называется критическим. Начиная с этого значения коэффициента трения, система совершает так называемое неколебательное движение. В этом случае движение происходит по закону:
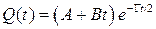, (3.6)
где А и В – константы.
Критическое затухание примечательно тем, что именно в этом случае осциллятор быстрее всего стремится к положению равновесия, причем, если коэффициент трения Г меньше критического, то он дойдет до положения равновесия быстрее, однако, при этом «проскочит» его по инерции. В этом случае осциллятор будет совершать колебания вблизи точки минимума.
При значениях Г больше критического (Г>2 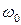) решение выглядит следующим образом:
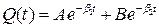, (3.7)
где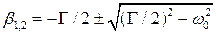 
. В этом случае осциллятор будет экспоненциально стремиться к положению равновесия, причем тем медленнее, чем больше трение.
Поскольку в электронно-конформационной модели 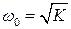, то критическое значение трения определяется как:
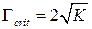. (3.8)
Величина коэффициента Г варьировалась выше и ниже критического значения 
. При фиксированном значении параметра К= 12 значение Г crit ≈6.8. При Г< Г crit наблюдались колебания системы вблизи минимума потенциала (рис. 3.4а, колебания отмечены пунктирным прямоугольником). При Г> Г crit наблюдался неколебательный случай динамики RyR-канала (рис. 3.4б)
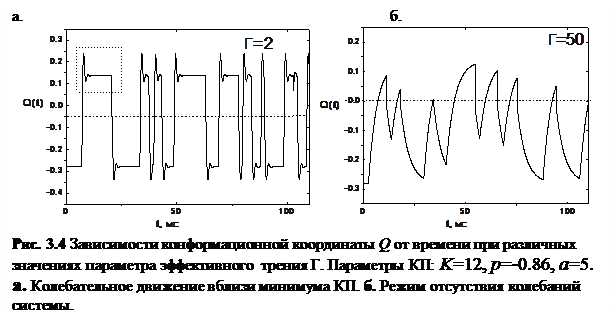
При проведении дальнейших численных экспериментов параметр Г выбирался по значению больше критического (Г=7).
3.2.2 Влияние коэффициента упругости канала K на форму конформационного потенциала
Конформационный потенциал (2.4) имеет два локальных минимума со следующими конформационными координатами:
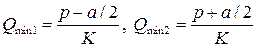. (3.9)
Первый минимум соответствует закрытому, второй - открытому состоянию канала. Положение этих минимумов зависит от величины коэффициента упругости К.
Варьируя значения К в широком интервале [1; 20] при фиксированном наборе остальных коэффициентов в (2.4), можно исследовать влияние этого параметра на свойства конформационного потенциала. Типичные графики конформационного потенциала представлены на рисунке 3.5.
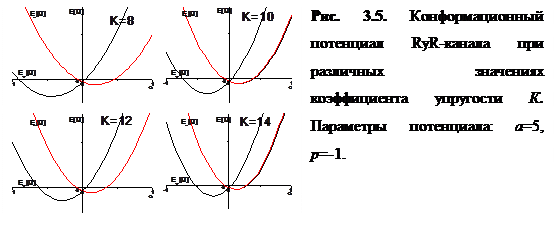
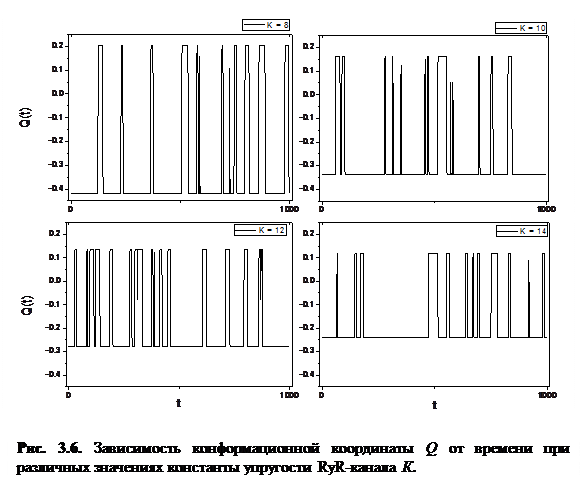
Как видно из рисунков 3.5 и 3.6, с увеличением значения коэффициента K уменьшается расстояние между минимумами КП и крутизна ветвей КП. При изучении конформационной динамики канала исследовалось среднее время релаксации канала из точки, соответствующей одному минимуму КП в другой минимум (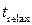
).
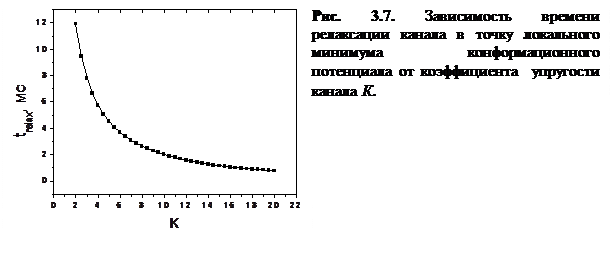
Как показывает график, представленный на рисунке 3.7, с ростом К уменьшается значение 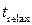. Другими словами, варьируя параметр К, можно менять скорости конформационной релаксации канала в ЭК-модели. В дальнейших экспериментах значение К выбиралось равным 12.
3.2.3 Зависимость конформационного потенциала от параметра электронно-конформационного взаимодействия а
Выбор интервала значений параметра а, характеризующего электронно-конформационное взаимодействие, а также изучение влияния этого параметра на форму потенциала (2.4) необходимы для успешного проведения компьютерных экспериментов.
При анализе влияния параметра а на свойства КП выбирался случай при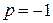 
, который соответствует условиям глобального минимума закрытого состояния канала. При этом значении p построены конформационные потенциалы при различных значениях параметра а и при К =12 (рис. 3.8).
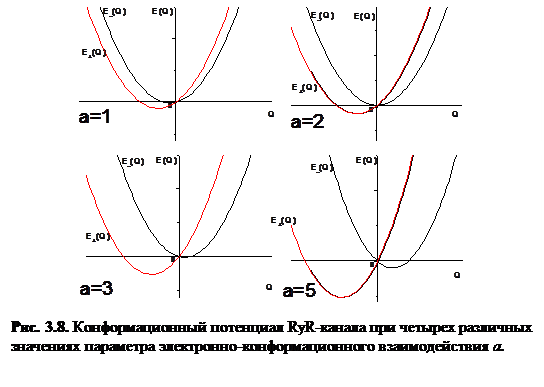
Как видно из графика, при а < 2 минимум правой ветви КП лежит левее точки пересечения ветвей КП, а это означает отсутствие локального минимума, отвечающего за открытое состояние RyR-канала.
Необходимо оценить интервал значений параметра а, при котором наблюдается стабильность правого локального минимума потенциала. Это условие выполняется в том случае, когда минимум находится правее точки пересечения ветвей потенциала. Данная точка имеет координаты (0;0). Правый минимум имеет координаты (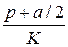
; 
), вследствие чего должно выполняться неравенство: 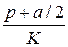>0.
Отсюда следует, что при минимальном значении параметра р =-1 безразмерный параметр а должен принимать значение больше 2. При проведении численных экспериментов, приведенных в данной работе, параметр а принимался равным 5.
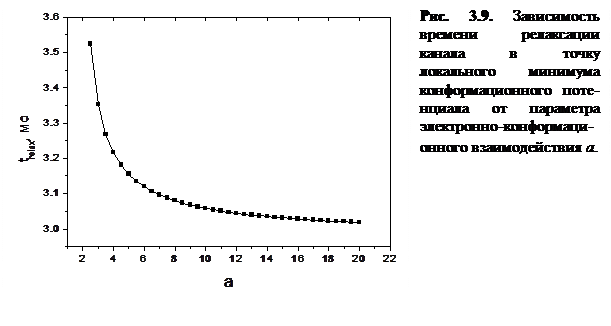
Как видно из рисунка 3.8, расстояние между минимумами КП увеличивается с ростом а, вследствие этого уменьшается время релаксации канала из одного локального минимума КП в другой (t relax) (рис. 3.9).
Date: 2015-08-24; view: 425; Нарушение авторских прав