Метод обертань Якобі

Чисельні методи є одним з потужних математичних засобів вирішення різних задач. Системи лінійних алгебраїчних рівнянь виникають як проміжний або остаточний етап при вирішенні ряду прикладних задач, що описуються диференціальними, інтегральними або системами нелінійних (трансцендентних) рівнянь. Вони можуть з'являтися як етап в задачах математичного програмування, статистичної обробки даних, апроксимації функцій, при дискретизації крайових диференціальних задач методом кінцевих різниць, методом кінцевих елементів, проекційними методами, в методі граничних елементів тощо.

Матриці виникають можуть мати різні структури і властивості. Уже зараз є потреба у вирішенні систем лінійних алгебраїчних рівнянь з матрицями повного заповнення порядку декількох тисяч. При вирішенні ряду прикладних задач методом кінцевих елементів в ряді випадків

з'являються системи, що володіють симетричними позитивно певними стрічковими матрицями порядку кілька десятків тисяч з половиною ширини стрічки до тисячі. І, нарешті, при використанні в ряді задач методу кінцевих різниць необхідно вирішити системи різницевих рівнянь з розрідженими матрицями порядку мільйон.

Одним з найпоширеніших методів вирішення систем лінійних рівнянь є метод обертань Якобі. Цей метод (який також називають методом простих ітерацій) відомий в різних варіантах вже більше 200 років. Розглянемо метод обертань Якобі[7] більш детально. В його основі лежить наступна теорема.

Якщо 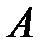– ермітова матриця, то існує така унітарна матриця 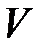, що перетворення подібності з цією матрицею 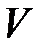приводить матрицю до діагонального вигляду, тобто , де 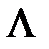- діагональна матриця власних значень матриць . Окремим випадком унітарної матриці є ортогональна матриця, для якої:

, 0, (1.7.1)

Позначимо через транспоновану матрицю. Так як 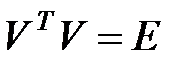, то тоді і отже перетворення подібності приймає вид. 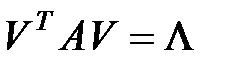. Задачу знаходження такої матриці 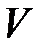вирішують за допомогою ітерації. Нехай А – дійсна симетрична матриця. Для такої матриці метод обертань полягає у побудові послідовності матриць, , таких що 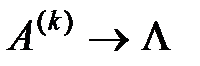. Тут кожна наступну матрицю отримують з попередньої за допомогою елементарного кроку, що складається в перетворенні подібності попередньої матриці за допомогою деякої ортогональної матриці обертання:

(1.7.2)

У матриці на діагоналі стоять одиниці всюди, крім - 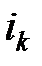і рядків і нулі вище і нижче головної діагоналі, крім двох елементів, так що елементи матриці 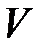описуються наступним чином:

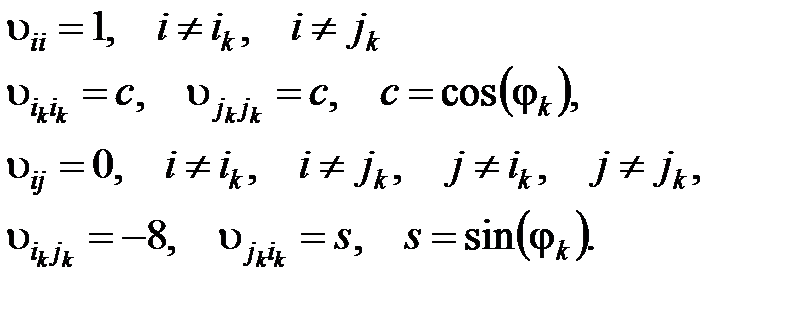(1.7.3)

При 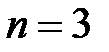, матриця буде мати вигляд

. (1.7.4)

Матриця будується з так, щоб виконувалась нерівність

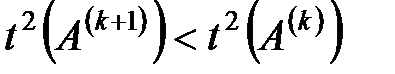, (1.7.5)

(1.7.6)

Можна показати, що при певному виборі

(1.7.7)

і отже .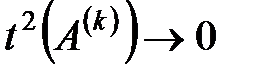

Для цього 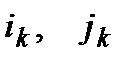вибираються як індекси максимального по модулю з над діагональних елементів матриці, тобто

(1.7.8)

а кут вибирається так, щоб

(1.7.9)

Звідси отримуємо

. (1.7.9)

Значення 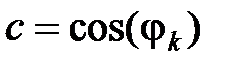і 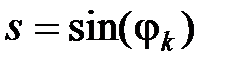можна обчислити і в такий спосіб:

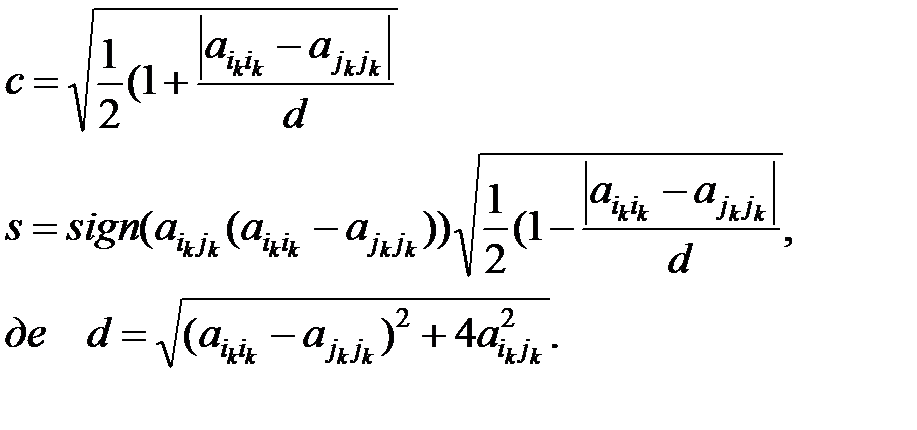(1.7.10)

Зауважимо, що якщо власні числа прості то тоді при цьому

(1.7.11)

Власні числа можна уточнити за наступною формулою:

(1.7.12)

Тоді (1.7.13)

Розглянемо формули для елементів матриці .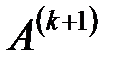

Позначимо (1.7.14)

Тоді очевидно, що у матриці зміняться тільки і 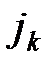стовпці, а у матриці 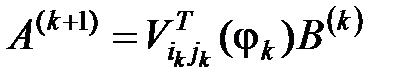зміняться тільки і рядки, так що в підсумку перераховуємо елементи тільки двох рядків або двох стовпців матриці за формулами:

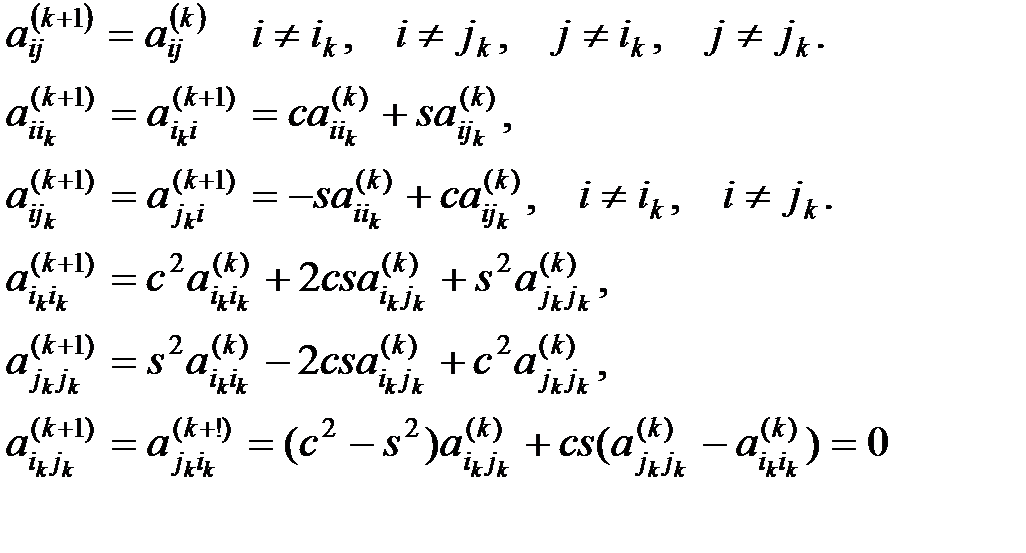
(1.7.15)

Очевидно, що власні вектори будуть стовпцями матриці

(1.7.16)

Отже, для знаходження власних значень слід скористатись наступним узагальненим алгоритмом.

Крок 1 Задати одиничну матрицю для обчислення власних векторів власних векторів 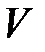. Задати матрицю 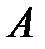та точність обчислення власних значень .

Крок 2 Знайти індекси найбільшого по модулю над діагонального елемента матриці : . Задати одиничну матрицю .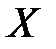

Крок 3 Обчислити величини

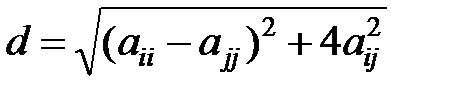(1.7.17)

(1.7.18)

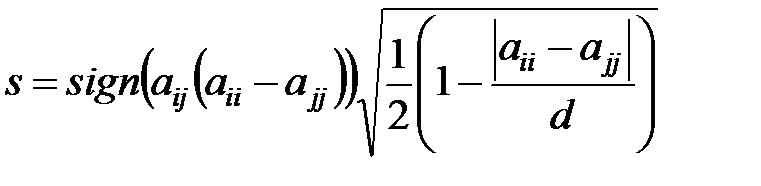(1.7.19)

Задати елементи матриці : , , .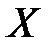

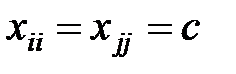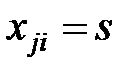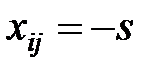Крок 4 Обчислити матрицю .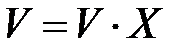

Крок 5 Обчислити матрицю .

Крок 6 Якщо 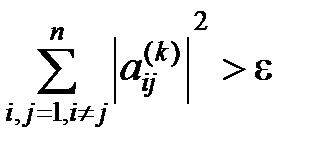, то перейти до кроку 2, інакше діагональні елементи матриці 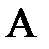- власні значення, а стовпці матриці 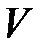- власні вектори.

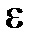З використанням цього алгоритму було розроблена підпрограма обчислення власних значень та власних векторів. Формальні параметри цієї підпрограми – симетрична матриця , точність обчислень та матриця власних векторів[7].

Date: 2015-08-24; view: 930; Нарушение авторских прав