Обчислення власних значень та власних векторів матриці

В цьому розділі розглядаються математичні методи, які лежать в основі ССА.

1) Метод обчислення власних значень та власних векторів матриці.

Розглянемо квадратну матрицю n-ого порядку:

(1.6.1)

Власні значення 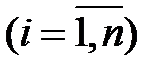квадратної матриці A є дійсні або комплексні числа, що задовольняють рівнянню:

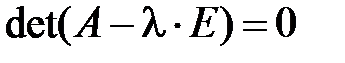, (1.6.2)

де E – одинична матриця.

Власні вектори обчислюються з розвязку системи рівнянь, що у матричній формі має вид:

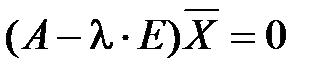(1.6.3)

де 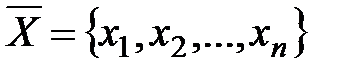- власний вектор матриці A, що відповідає деякому власному значенню .

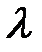Матриця 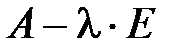називається характеристичною матрицею. Так як у матриці на головній діагоналі стоять 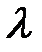, а всі інші елементи рівні нулю, то характеристична матриця має вигляд:

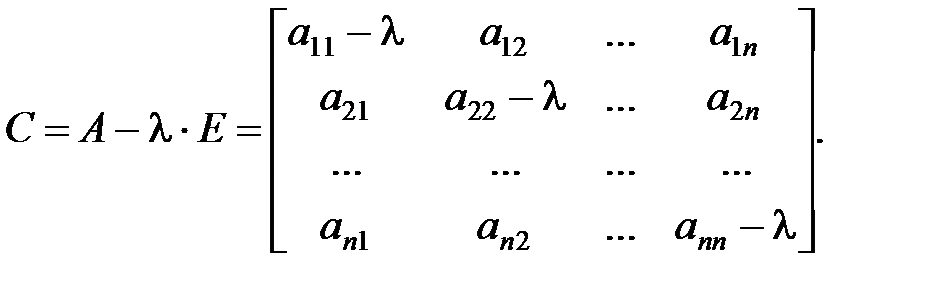(1.6.4)

Визначник цієї матриці називається характеристичним визначником:

(1.6.5)

У розгорнутому вигляді матриця є многочленом -го ступеня щодо , так як при обчисленні цього визначника добуток елементів головної діагоналі дає многочлен зі старшим членом 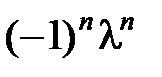, тобто

(1.6.6)

що називається характеристичним многочленом. Корені цього многочлена – власні значення або характеристичні числа матриці A.

Числа називаються коефіцієнтами характеристичного многочлена.

Ненульовий вектор 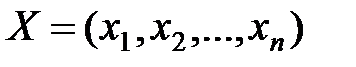називається власним вектором матриці A, якщо ця матриця переводить вектор 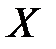в вектор 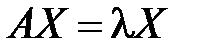, тобто добуток матриці A на вектор 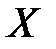і добуток характеристичного числа 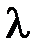на вектор є один і той же вектор. Кожному власному значенню i

матриці відповідає свій власний вектор 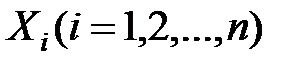.Для визначення координат власного вектора складається характеристичне рівняння:

(1.6.7)

Переписавши його у векторному вигляді і виконавши множення, отримаємо систему лінійних однорідних рівнянь:

(1.6.8)

Визначник цієї системи дорівнює нулю, тому з цієї умови були визначені власні значення матриці 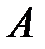. Отже, система має нескінченну множину рішень. Її можна вирішити з точністю до постійного множника (як систему однорідних рівнянь). Вирішивши цю систему, ми знайдемо всі координати власного вектора . Підставляючи у систему однорідних рівнянь по черзі 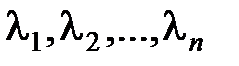, отримуємо 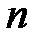власних векторів[7].

Date: 2015-08-24; view: 889; Нарушение авторских прав