Характеристика застосування для сингулярного спектрального аналізу

Для сингулярного спектрального аналізу розроблено спеціальне застосування. Воно складається з таких компонентів:

- підпрограма побудови траєкторної матриці;

- підпрограма обчислення власних значень і власних векторів;

- підпрограма сортування власних значень у порядку зменшення та відповідного сортування власних векторів;

- підпрограма діагонального усереднення для обчислення адитивних компонентів часового ряду.

На рисунку 3.1 наведено інтерфейс застосування.

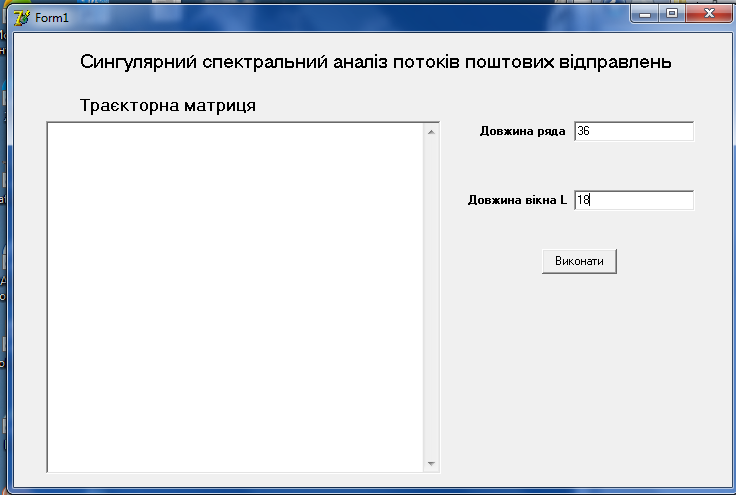
Рисунок 3.1 Інтерфейс застосування ССА

В даному застосуванні спочатку заносимо дані текстового файлу в

hystarray1. Потім вказуємо довжину ряду та довжину вікна. Після виконання даної операції виникають такі файли С_SV, SV_1_fv і SV_1_hystarray2, де записані власні та факторні вектори, відповідний компонент ряду. С_SV.txt – це файл, який містить в собі всі власні значення та власні вектори. Щоб провести аналіз компонента часового ряду потрібно файл С_SV. відкрити у Excel. Потім встановлюється

власний вектор, який відповідає максимальному власному значенню, а за тим відкривається файл у Excel, який містить адитивну компонентну часового ряду, що відноситься до першої сингулярної трійці.

3.2 Аналіз динаміки обсягу поштової кореспонденції у Ширяївському ЦПЗ №4 Одеської дирекції УДППЗ «Укрпошта»

Розглянемо динаміку обсягів поштової кореспонденції за весь 2013 р., де максимальному власному значенню відповідає факторний вектор, власний вектор і відповідний компонент ряду. Для сингулярного розкладання і виділення тренду сама траєкторна матриця формується для вікна з довжиною, яка дорівнює половині періоду спостереження .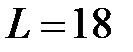

Розглянемо сингулярне розкладання часових рядів, що описують динаміку обсягів вхідних поштових відправлень, де максимальне власне значення – .

В результаті виконання процедури сингулярного спектрального аналізу (ССА) побудуємо власний та факторний вектори і адитивний компонент ряду, які відповідають максимальному власному значенню 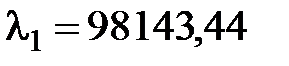потоку вхідних рекомендованих бандеролей (РБ).

Рисунок 3.2 – Власний вектор часового ряду вхідних рекомендованих бандеролей

На рис. 3.2 наведено графік компонент першого власного вектора часового ряду рекомендованих бандеролей. На даному рисунку 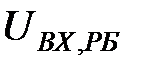- це значення компоненти власного вектора, а - номер компоненти ряда. На даному рисунку спостерігається збільшення значень компоненти власного вектора. Це пов’язано з сезонним коливанням попиту на цю послугу.

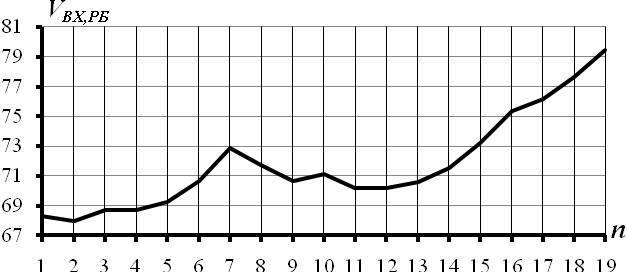
Рисунок 3.3 – Факторний вектор часового ряду вхідних рекомендованих бандеролей

На рис. 3.3 наведено графік компонент першого факторного вектора часового ряду рекомендованих бандеролей. На даному рисунку 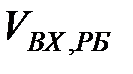- це значення компонент факторного вектора. Компоненти факторного вектора спочатку зростають, а потім спадають і знову зростають.

Рисунок 3.4 – Перший адитивний компонент часового ряду вхідних рекомендованих бандеролей

На рис. 3.4 наведено графік першої адитивної компоненти часового ряду рекомендованих бандеролей, або тренду. На даному рисунку 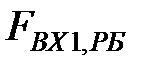- це значення обсягів вхідних рекомендованих бандеролей. Збільшення значень тренду рекомендованих бандеролей під кінець року мають сезонний характер.

Проаналізуємо часовий ряд вхідних простих бандеролей (ПБ). Максимальне власне значення для цього ряду – .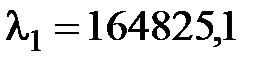

Рисунок 3.5 – Власний вектор часового ряду вхідних простих бандеролей

На рис. 3.5 наведено графік компонент першого власного вектора часового ряду простих бандеролей. На даному рисунку 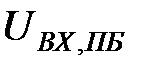– це значення компоненти власного вектора. Компоненти цього вектора лінійно збільшуюються.

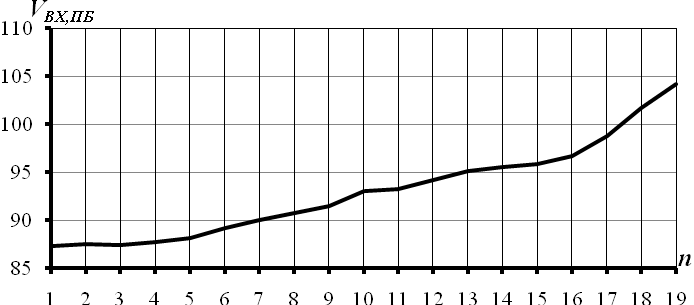
Рисунок 3.6 Факторний вектор часового ряду вхідних простих бандеролей

На рис. 3.6 наведено графік компонент першого факторного вектора часового ряду простих бандеролей. На даному рисунку 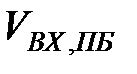- це значення компоненти факторного вектора. З даного рисунку видно, що компоненти факторного вектора лінійно збільщуються.

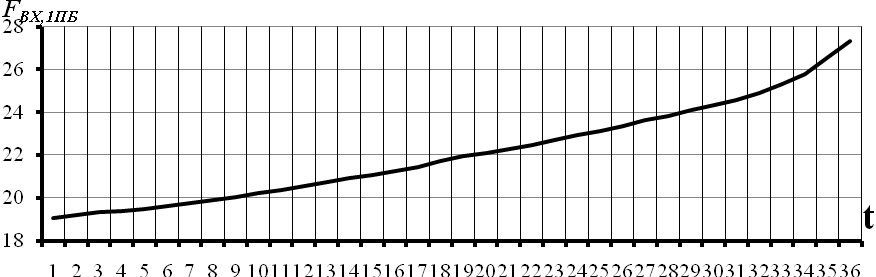
Рисунок 3.7 – Перший адитивний компонент часового ряду вхідних простих бандеролей

На рис 3.7 наведено графік першої адитивної компоненти часового ряду простих бандеролей або тренду. На даному рисунку 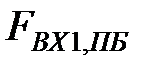- це значення обсягів вхідних простих бандеролей. З даного рисунку слідує, що значення тренда простих бандеролей мають лінійну залежність від часу і спостерігається тенденція до збільшення.

Проаналізуємо часовий ряд вхідних простих листів (ПЛ). Максимальне власне значення цього ряду – .

Рисунок 3.8 – Власний вектор часового ряду вхідних простих листів

На рис 3.8 наведено графік компонент першого власного вектора часового ряду простих листів. На даному рисунку - це значення компоненти власного вектора. Компоненти власного вектора змінюються нелінійно.

Рисунок 3.9 – Факторний вектор часового ряду вхідних простих листів

На рис 3.9 наведено графік компонент першого факторного вектора часового ряду простих листів. На даному рисунку 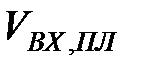- це значення компоненти факторного вектора. На даному рисунку спостерігається, що компоненти факторного вектора на початку мають приблизний вид до лінійного характеру, але потім різко спадають і знову зростають. Це пояснюється новорічними святами та початком навчального року. Компоненти факторного вектора мають нелінійний характер.

Рисунок 3.10 – Перша адитивна компонента часового ряду вхідних простих листів

На рис 3.10 наведено графік першого адитивного компонента часового ряду часового ряду простих листів або тренду. На даному рисунку - це значення обсягів вхідних простих листів. З даного рисунку слідує, що значення тренда має деяку неперіодичність. Під кінець року спостерігається тенденція до збільшення. Це визвано початком навчального року та наступаючими новорічними святами.

Проаналізуємо часовий ряд вхідних рекомендованих листів (РЛ). Максимальне власне значення цього ряду – .

Рисунок 3.11 – Власний вектор часового ряду вхідних рекомендованих листів

На рис. 3.11 наведено графік компонент першого власного вектора часового ряду рекомендованих листів. На даному рисунку 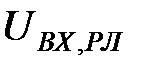- це значення компоненти власного вектора. Компоненти власного вектора коливаються дуже стохастично і змінюються нелінійно. Спостерігається тенденція до збільшення.

Рисунок 3.12 – Факторний вектор часового ряду вхідних рекомендованих листів

На рис. 3.12 наведено графік компонент першого факторного вектора часового ряду рекомендованих листів. На даному рисунку 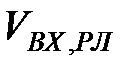- це значення компоненти факторного вектора. Спостерігається значне спадання компоненти факторного вектора, а потім збільшення.

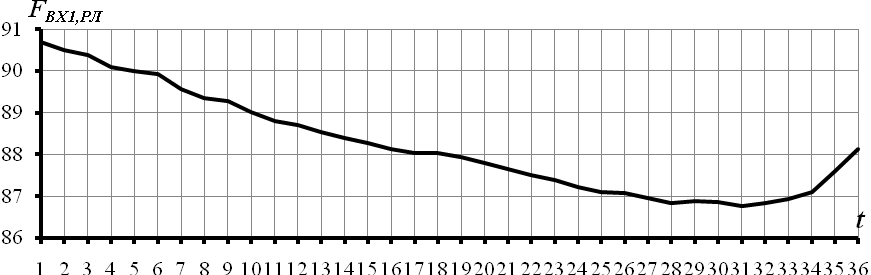
Рисунок 3.13 – Перший адитивний компонент часового ряду вхідних рекомендованих листів

На рис. 3.13 наведено графік першого адитивного компонента часового ряду рекомендованих листів або тренду. На даному рисунку 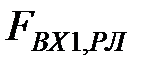- це значення обсягів вхідних рекомендованих листів. З рисунку можна зробити висновок, що значення тренда рекомендованих листів поступово спадають, а вже під кінець року збільшуються.

Проаналізуємо часовий ряд вхідних посилок (П). Максимальне власне значення для цього ряду – .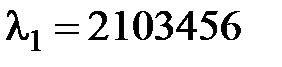

Рисунок 3.14 –Власний вектор часового ряду вхідних посилок

На рис. 3.14 наведено графік компонент першого власного вектора часового ряду посилок. На даному рисунку - це значення компоненти власного вектора. З наведеного рисунку слідує, що компоненти власного вектора коливаються з різними інтервалами.

Рисунок 3.15 –Факторний вектор часового ряду вхідних посилок

На рис. 3.15 наведено графік компонент першого факторного вектора часового ряду посилок. На даному рисунку 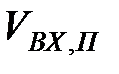- це значення компоненти факторного вектора. З даного рисунку слідує, що компоненти факторного вектора спадають, а потім зростають.

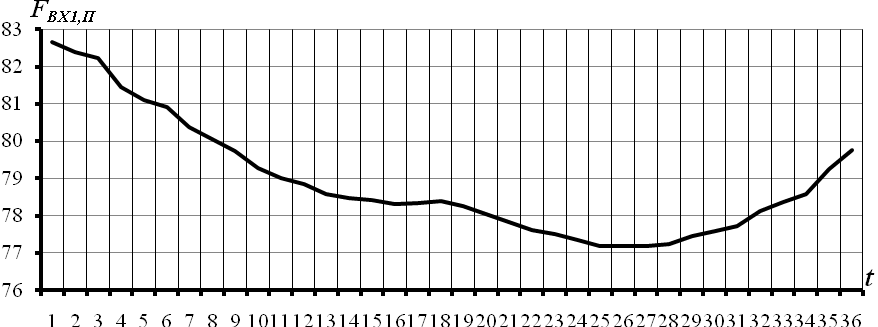
Рисунок 3.16 –Перший адитивний компонент часового ряду вхідних посилок

На рис. 3.16 наведено графік першого адитивного компонента часового ряду посилок або тренду. На даному рисунку - це значення обсягів вхідних посилок. Значення тренда посилок поступово спадають, а з жовтня збільшуються.

Проаналізуємо часовий ряд вихідних простих бандеролей (ПБ). Максимальне власне значення цього ряду – .

Рисунок 3.17 – Власний вектор часового ряду вихідних простих бандеролей

На рис. 3.17 наведено графік компонент першого власного вектора часового ряду простих бандеролей. На даному рисунку 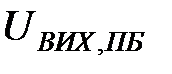- це значення компоненти власного вектора. З даного рисунку слідує, що компоненти власного вектора змінюються з різними інтервалами.

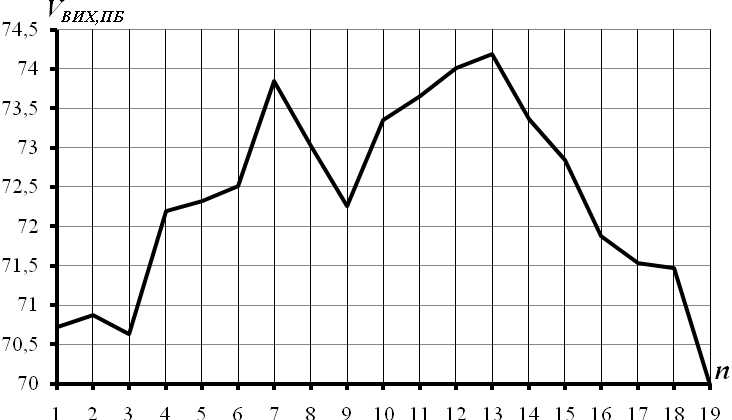
Рисунок 3.18 –Факторний вектор часового ряду вихідних простих бандеролей

На рис 3.18 наведено графік компонент першого факторного вектора часового ряду простих бандеролей. На даному рисунку 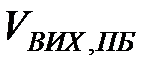- це значення компоненти факторного вектора. З наведеного рисунку видно, що компоненти факторного вектора зростають і спадають.

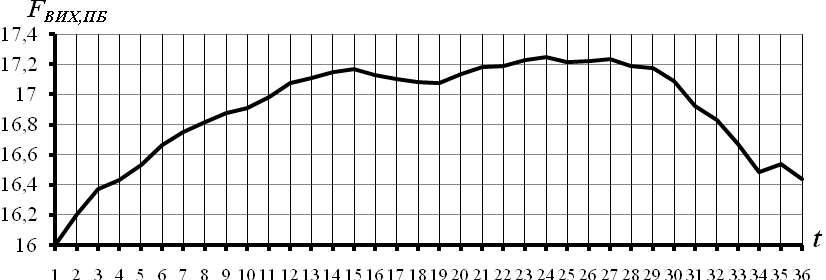
Рисунок 3.19 – Перший адитивний компонент часового ряду вихідних простих бандеролей

На рис. 3.19 наведено графік першого адитивного компонента часового ряду простих бандеролей або тренду. На даному рисунку 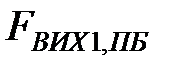- це значення обсягів вихідних простих бандеролей. Значення тренда простих бандеролей мають нелінійну залежність в часі.

Проаналізуємо часовий ряд вихідних рекомендованих бандеролей (РБ). Максимальне власне значення для цього ряду – .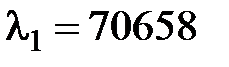

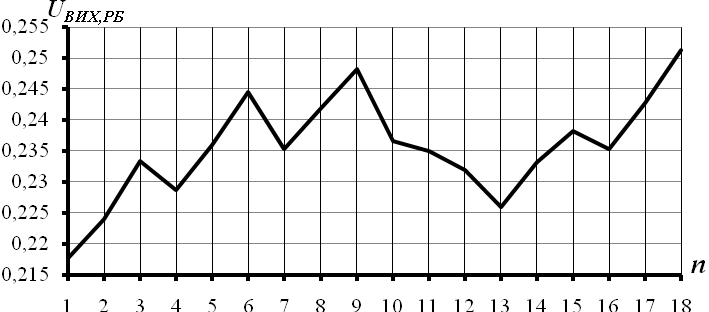
Рисунок 3.20 – Власний вектор часового ряду вихідних рекомендованих бандеролей

На рис. 3.20 наведено графік компонент першого власного вектора часового ряду рекомендованих бандеролей. На даному рисунку - це значення компоненти власного вектора. З наведеного рисунку слідує, що компоненти власного вектора поступово зростають і спадають, але потім знову зростають.

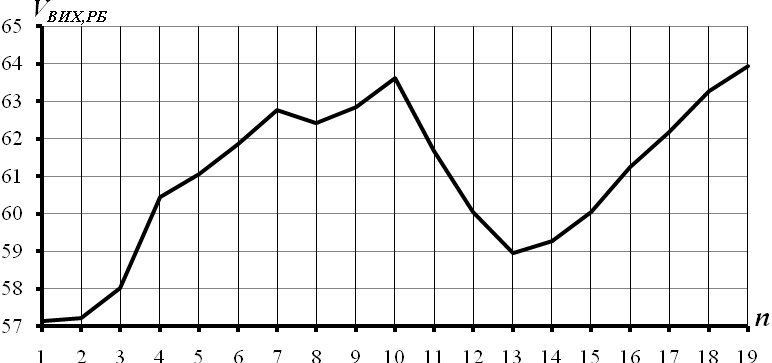
Рисунок 3.21 – Факторний вектор часового ряду вихідних рекомендованих бандеролей

На рис. 3.21 наведено графік компонент першого факторного вектора часового ряду рекомендованих бандеролей. На даному рисунку 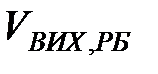- це значення компоненти факторного вектора. Як видно з наведеного рисунку, що компоненти факторного вектора зростають і потім спадають, а потім знову зростають.

Рисунок 3.22 – Перший адитивний компонент часового ряду вихідних рекомендованих бандеролей

На рис. 3.22 наведено графік першого адитивного компонента часового ряду рекомендованих бандеролей або тренду. На даному рисунку 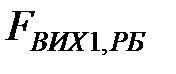- це значення обсягів вихідних рекомендованих бандеролей. На даному рисунку спостерігається поступове зростання значення тренду вихідних рекомендованих бандеролей.

Проаналізуємо часовий ряд вихідних простих листів (ПЛ). Максимальне власне значення цього ряду – .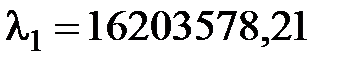

y ZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAHaR0X3dAAAABQEAAA8AAAAAAAAAAAAAAAAATAIAAGRy cy9kb3ducmV2LnhtbFBLAQItABQABgAIAAAAIQCWVR8AAAEAACoCAAAOAAAAAAAAAAAAAAAAAFYD AABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQCrFs1GuQAAACIBAAAZAAAAAAAAAAAAAAAA AIIEAABkcnMvX3JlbHMvZTJvRG9jLnhtbC5yZWxzUEsBAi0AFAAGAAgAAAAhAD8LZYAkAQAAkwEA ACAAAAAAAAAAAAAAAAAAcgUAAGRycy9jaGFydHMvX3JlbHMvY2hhcnQxLnhtbC5yZWxzUEsBAi0A FAAGAAgAAAAhAHQ1A64BBwAA4BoAABUAAAAAAAAAAAAAAAAA1AYAAGRycy9jaGFydHMvY2hhcnQx LnhtbFBLBQYAAAAABwAHAMsBAAAIDgAAAAA= ">

Рисунок 3.23 –Власний вектор часового ряду вихідних простих листів

На рис. 3.23 наведено графік компонент першого власного вектора часового ряду простих листів. На даному рисунку 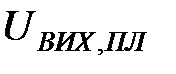- це значення компоненти власного вектора. З наведеного рисунку можна зробити висновок, що компоненти власного вектора коливаються в різних інтервалах.

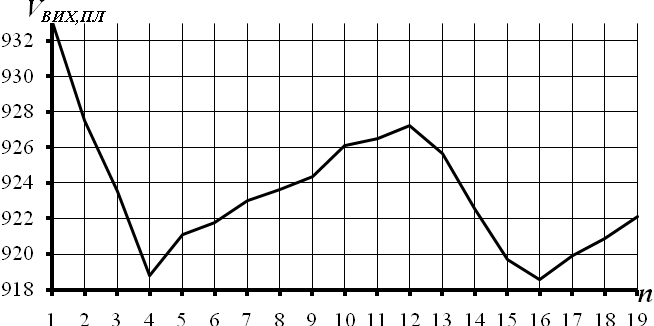
Рисунок 3.24 – Факторний вектор часового ряду вихідних простих листів

На рис. 3.24 наведено графік компонент першого факторного вектора часового ряду простих листів. На даному рисунку - це значення компоненти факторного вектора. Компоненти факторного вектора сильно спадають на початку спадають і потім зростають.

Рисунок 3.25 – Перший адитивний компонент часового ряду вихідних простих листів

На рис. 3.25 наведено графік першого адитивного компонента часового ряду простих листів або тренду. На даному рисунку - це значення обсягів вихідних простих листів. З наведеного рисунку можна зробити висновок, що значення тренда простих листів спадають на початку року і тільки з грудня збільшуються.

Проаналізуємо часовий ряд вихідних рекомендованих листів (РЛ). Максимальне власне значення цього ряду – .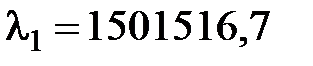

Рисунок 3.26 – Власний вектор часового ряду вихідних рекомендованих листів

На рис. 3.26 наведено графік компонент першого власного вектора часового ряду рекомендованих листів. На даному рисунку 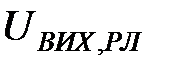- це значення компоненти власного вектора. Компоненти власного вектора коливаються з різними інтервалами.

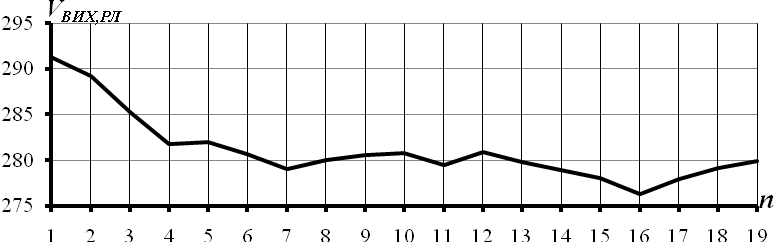
Рисунок 3.27 – Факторний вектор часового ряду вихідних рекомендованих листів

На рис. 3.27 наведено графік компонент першого факторного вектора часового ряду рекомендованих листів. На даному рисунку 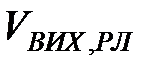- це значення компоненти факторного вектора. З наведеного рисунку слідує, що компоненти факторного вектора змінюються нелінійно.

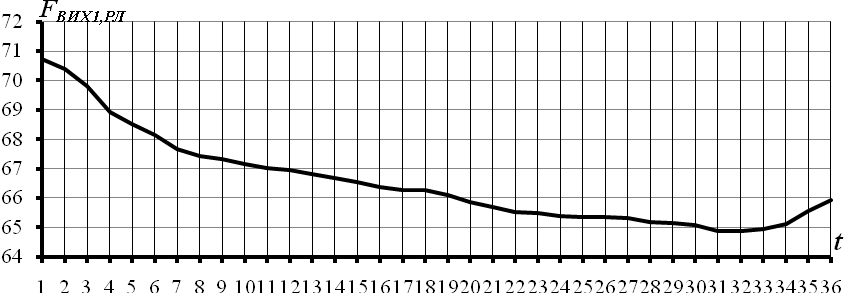
Рисунок 3.28 – Перший адитивний компонент часового ряду вихідних рекомендованих листів

На рис. 3.28 наведено графік першого адитивного компонента часового ряду рекомендованих листів або тренду. На даному рисунку - це значення обсягів вихідних рекомендованих листів. З наведеного рисунку слідує, що значення тренда рекомендованих листів поступово зменшуються і на початку наступного року можна очікувати збільшення.

Проаналізуємо часовий ряд вихідних посилок (П). Максимальне власне значення для цього ряду – .

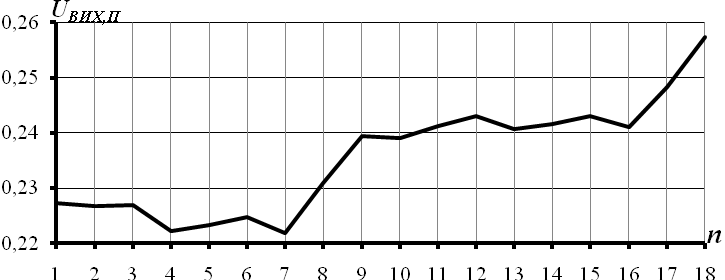
Рисунок 3.29 – Власний вектор часового ряду вихідних посилок

На рис. 3.29 наведено графік компонент першого власного вектора часового ряду посилок. На даному рисунку 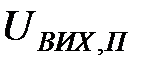- це значення компонентивласного вектора. З наведеного рисунку видно, що компоненти власного вектора поступово збільшуються.

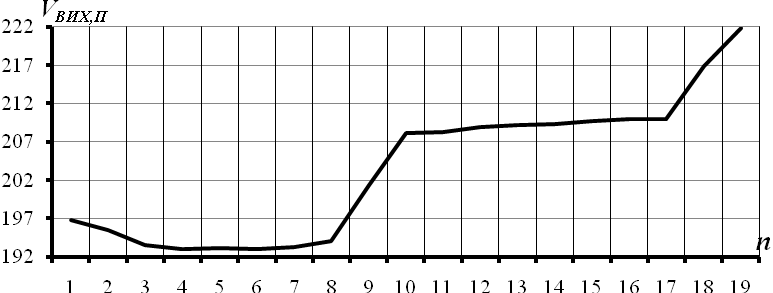
Рисунок 3.30 – Факторний вектор часового ряду вихідних посилок

На рис. 3.30 наведено графік компонент першого факторного вектора часового ряду посилок. На даному рисунку - це значення

Компоненти факторного вектора. Компоненти факторного вектора спадають, а потім зростають.

Рисунок 3.31 – Перший адитивний компонент часового ряду вихідних посилок

На рис. 3.31 наведено графік першого адитивного компонента часового ряду посилок або тренду. На даному рисунку - це значення обсягу вихідних посилок. З наведеного рисунку слідує, що значення тренда посилок з середини березня зростають. Вид тренда близький до лінійної залежності.

Date: 2015-08-24; view: 412; Нарушение авторских прав