Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теорема об изменении количества движения точки. Количеством движения точки называется вектор, равный произведению массы точки на её скорость - (рис
|
|
Количеством движения точки называется вектор, равный произведению массы точки на её скорость -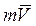 
(рис. 12).
Запишем основное уравнение динамики: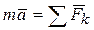 
, или 
. Внеся массу под знак дифференциала (m = const), получим теорему об изменении количества движения точки в дифференциальной форме: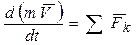 
- производная по времени от количества движения точки равна сумме сил, действующих на нее. Разделяя переменные и интегрируя, имеем 
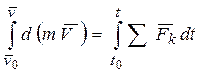. Поменяв местами действия суммирования и интегрирования в правой части уравнения, взяв интеграл в левой части уравнения и обозначив: 
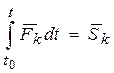,получим теорему об изменении количества движения точки в интегральной форме:
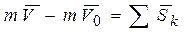(26)
Вектор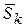 
называется импульсом силы. если 
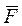= const, то 
.
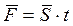изменение количества движения точки за некоторый промежуток времени равно сумме импульсов сил, действующих на неё за тот же промежуток времени.
теорема об изменении количества движения точки векторная, ее можно записать в проекциях на оси координат:
;
;
.
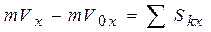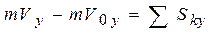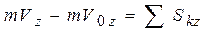Date: 2015-08-15; view: 400; Нарушение авторских прав