Свободные колебания

Свободными называются колебания точки, происходящие под действием только восстанавливающей силы. Сила называется восстанавливающей, если она все время стремится вернуть точку в положение равновесия. Примером восстанавливающей силы является сила упругости пружины. Если восстанавливающая сила пропорциональна смещению точки из положения равновесия, то она называется линейной восстанавливающей силой.

Пусть на точку М массой m действует линейная восстанавливающая сила упругости (рис. 2): F_упр = сΔ, где с – жесткость пружины (физический смысл жесткости - это сила, необходимая для деформации пружины на единицу длины), в Н/м; Δ – деформация пружины, м.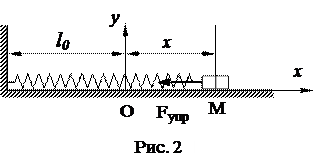

На рис. 2 l₀ – длина недеформированной пружины. Выбрав начало координат в положении равновесия – т. О, запишем основное уравнение динамики в проекции на ось x: 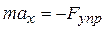, или .

Отсюда получим 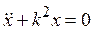(4)

Выражение (4) – это и есть уравнение свободных колебаний точки. Здесь 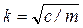называется круговой частотой колебаний (физический смысл: число колебаний за 2π секунд), с^-1. Общее решение дифференциального уравнения (4) имеет вид:

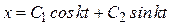. (5)

Взяв производную по времени, имеем

. (6)

Постоянные интегрирования С ₁ и С ₂ найдем из начальных условий:

при 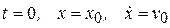. (7)

Подставив (7) в (5) и (6), находим .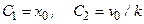

С учетом этого решение (5) принимает вид:

. (8)

Решение (8) можно записать в виде:

, (9)

где 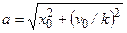- амплитуда колебаний, м; - начальная фаза колебаний, рад.

Из (9) видно, что свободные колебания являются гармоническими. Период колебаний можно найти по формуле:

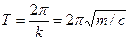. (10)

Date: 2015-08-15; view: 732; Нарушение авторских прав