Закон всемирного тяготения

Сила, с которой два тела притягиваются друг к другу, называется силой

тяготения или гравитационной силой. Гравитационное взаимодействие связано с наличием массы у взаимодействующих тел и описывается законом всемирного тяготения – две материальные точки с массами m1 и m2 притягиваются по направлению друг к другу каждая с силой, прямо пропорциональной массам этих точек и обратно пропорциональной квадрату расстояния r между ними:

m₁ m₂

F = G 2-----------

R² (5.1)

где G - постоянная тяготения Ньютона или гравитационная постоянная,

m1 и m2 - гравитационные массы.

Гравитационная постоянная численно равна силе, с которой взаимодействуют две материальные точки с единичной массой, расположенные на единичном расстоянии друг от друга.

Для нахождения сил тяготения, действующих на протяжённые тела, необходимо мысленно разбить эти тела на элементарные кусочки, которые можно принять за материальные точки. Затем находят силы взаимодействия между ними и, векторно складывая их, получают результирующую силу, действующую на каждое из тел. Если два тела являются однородными шарами, то они притягиваются как материальные точки, расположенные в их центрах и имеющие массы соответствующих тел. В частности, Землю принимают за однородный шар радиусом RЗ = 6 400 км.

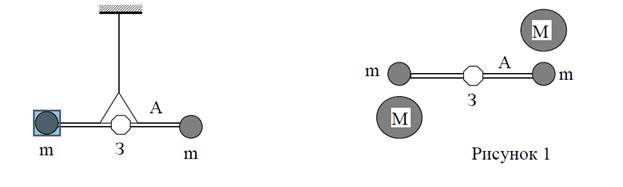
Во времена Ньютона закон всемирного тяготения был подтверждён только астрономическими наблюдениями над движениями планет и их спутников. Впервые непосредственное экспериментальное доказательство этого закона для земных тел, атакже численное определение гравитационной постоянной G были даны английским физиком Кавендишем в 1798 г. Схема прибора Кавендиша показана на рисунке 1. На концах сравнительно легкого коромысла А находились два одинаковых свинцовых шарика, каждый массой m. Коромысло подвешивалось за середину на достаточно длинной тонкой упругой нити. К середине коромысла было прикреплено зеркальце З. Поворот луча света, отражённого от зеркальца, отмечает закручивание нити, на которой подвешено коромысло А. К массам m придвигались с разных сторон на определённое расстояние два больших свинцовых шара с массой М каждый, причем M >> m. Под действием сил тяготения коромысло А крутильных весов поворачивалось до тех пор, пока момент силы тяготения между шарами не уравновешивался упругим моментом закрученной нити, который и определялся по смещению зайчика, отражённого от зеркальца. Устанавливая массы на различных расстояниях, Кавендиш определил силу тяготения в зависимости от расстояния и подтвердил справедливость закона всемирного тяготения, выведенного Ньютоном. Зная упругие свойства нити и массы шаров, Кавендиш вычислил значение гравитационной постоянной.

Существуют и другие методы определения гравитационной постоянной. На

основании опытов в настоящее время для гравитационной постоянной принимается следующее значение G = 6,672*10^-11 м³/(кг*с2). Полученный Кавендишем результат отличается от современного значения гравитационной постоянной только на 1 %.

Формулируя закон тяготения (5.1), мы молчаливо предполагали, что масса тела, входящая в этот закон, есть та же масса, которая является мерой инерции. Это действительно так, поскольку все современные методы определения массы указывают на то, что с очень большой степенью точности значения гравитационной и инертной массы совпадают.

Сила тяжести. Под действием силы притяжения к Земле все тела падают с

одинаковым относительно поверхности Земли ускорением, равным ускорению сво-

бодного падения g. Это означает, что в системе отсчёта, связанной с Землёй, на каж-

дое тело массой m согласно второму закону Ньютона действует сила:

F = mg, (5.2)

называемая силой тяжести.

Итак, под действием силы тяжести (без учёта действия других сил, например,

силы сопротивления воздуха) все тела в одном и том же поле тяготения падают с

одинаковым ускорением g. Следовательно, в данном месте Земли ускорение сво-

бодного падения не зависит от массы и одинаково для всех тел.

В случае Земли ускорение свободного падения изменяется от 9,780 м/с2 на

экваторе до 9,832 м/с2 на полюсах. Это различие обусловлено суточным вращением

Земли вокруг своей оси и сплюснутостью Земли (экваториальный и полярный ра-

диусы Земли равны 6 378 км и 6 357 км, соответственно). Различие в значениях

ускорения силы тяжести на экваторе и на полюсах очень мало (оно не превышает

0,5 %), поэтому в первом приближении Землю можно считать однородным шаром

радиуса RЗ, а силу тяжести можно считать равной силе, с которой тело притягивает-

ся к Земле, а ускорение свободного падения, которое используется при решении

практических задач, принимают равным 9,81 м/с2.

Если тело массы m находится вблизи поверхности Земли, то ускорение сво-

бодного падения g телу сообщается силой тяготения Fгр. И согласно второму закону

Ньютона

g =

m

Fгр =

m

1 G 2

З

З

R

mM = G 2

З

З

R

M. (5.3)

Получили выражение (5.3) для g, не зависящее от массы тела, т.е. одинаковое для

всех тел. При этих же рассуждениях можно получить выражение для g(h)  уско-

ренния свободного падения на высоте h над поверхностью Земли:

g(h) = G  2

З

З

R h

M



. (5.4)

Выражая произведение GMЗ из выражения (5.3) и подставляя в (5.4), имеем:

g(h) = G  2

З

З

R h

M



= g  2

З

З

R h

R



= g

З

З

R h

R

 



 





= g

З R

1 h



 



 



, (5.5)

где g – ускорение свободного падения у поверхности Земли.

В идеале свободное падение должно происходить в безвоздушном

пространстве, что исключает силу сопротивления атмосферного воздуха. Для

плотных тел небольших размеров (при малых скоростях их движения) влияние

атмосферы незначительно и не может заметно повлиять на величину ускорения

свободного падения, но сказывается при падении лёгких объёмных тел. Именно из-

за сопротивления воздуха различные тела падают с раличными ускорениями.

Вес тела – это сила, с которой тело действует на неподвижное относительно

него горизонтальную опору или вертикальный подвес, удерживающие тело от

падения вследствие притяжения к планете. Нужно отметить, что вес P – это сила,

приложенная к опоре (подвесу), а не к телу. И по третьему закону Ньютона вес

равен силе упругости (силе реакции опоры или подвеса) N, приложенной к телу, т.е.

P = - N. На покоящееся относительно опоры (подвеса) тело действуют сила тяжести

F и сила реакции опоры (сила упругости подвеса) N (см. рисунок 2). Вес P и сила

тяжести F приложены к различным

объектам, к опоре и к телу, поэтому

они не могут уравновешивать друг

друга. Помимо этого они имеют

различную физическую природу,

соответственно, вес – упругую, т.е.

по существу электромагнитную природу, а сила тяжести – гравитационную. Таким

образом, сила тяжести действует всегда, а вес тела проявляется только в том случае,

когда на тело кроме силы тяжести действуют ещё другие силы.

В частном случае, когда опора (подвес) покоится или движется равномерно и

прямолинейно относительно какой-либо инерциальной системы отсчёта, вес тела P

по величине и направлению совпадает с силой тяжести m g, т.е.

P = m g. (5.6)

Если, например, ускорение а тела направлено вертикально вверх, то второй за-

кон Ньютона для тела в векторной форме записи имеет вид (см. рисунок 2):

N

F P

F

N

P

Рисунок 2

у

а

m a = N + F = N + m g. (5.7)

Уравнение (5.7) в проекции на вертикальную ось 0у примет вид:

m a = N  F = N  mg, (5.8)

откуда

N = m(g + a). (5.9)

И вес тела, равный

P = N = m(g + a), (5.10)

оказывается больше силы тяжести mg. Кратность перегрузки равна

 

g

g a

mg

m g a

F

P 





  1. (5.11)

В данном примере направления векторов веса тела P и силы тяжести F = m g совпа-

дают.

Если же ускорение тела а направлено вертикально вниз (т.е. а по направлению

совпадает с направлением g), то вес тела, равный по модулю

P = m(g  a), (5.12)

оказывается меньше веса покоящегося тела (mg). При свободном падении тела, а =

g, и P = 0, т.е. вес отсутствует. Наступает состояние невесомости. Следовательно,

если на тело действует только сила тяжести, т.е. когда оно свободно падает, тело на-

ходится в состоянии невесомости.

В общем случае если тело свободно движется в поле тяготения (в этом случае

на тело действует только сила тяжести) по любой траектории и в любом направле-

нии, то а = g, и из уравнения (5.7) следует, что

P =  N = F  m a = m g  m a = m(g  a) = 0,

т.е. тело будет невесомым. Например, невесомыми являются тела, находящиеся в

космических кораблях, свободно движущихся в космосе.

При движении тела вертикально вниз с ус-

корением а в случае  а   g  (т.е. при a  g)

уравнение движение тела имеет вид (см. рису-

нок 3):

m a = N + F = N + m g. 5.13)

Запишем уравнение (5.13) в проекции на вертикальную ось 0у:

m a = N + F = N + mg, (5.14)

откуда

N = m(а  g). (5.15)

И вес тела, равный

P = N = m(а  g), (5.16)

опять станет отличным от нуля. Причём направление вектора веса тела P в этом

случае окажется противоположно направлению вектора ускорения свободного па-

дения g (см. рисунок 3).

Космические скорости. Спутник Земли всегда движется в плоскости, прохо-

дящей через центр Земли. Если в качестве модели Земли выбрать однородный шар,

то ориентация плоскости не изменяется. В зависимости от начальных условий спут-

ник (или какое-либо тело) будет двигаться по гиперболе, параболе, эллипсу или по

отрезку прямой линии. Частный случай эллипса – окружность. Для запуска спутни-

g

P

Рисунок 3

F N

a

у

ков в космическое пространство в зависимости от поставленных целей необходимо

сообщать им определённые начальные скорости, называемые космическими.

Первая космическая скорость v1 – это скорость, которую необходимо сооб-

щить телу вблизи поверхности Земли в горизонтальном направлении, перепендику-

лярном радиусу окружности, т.е. радиусу Земли

RЗ, чтобы оно стало двигаться по этой окружности,

т.е. превратилось в искусственный спутник Земли.

В этом случае тело двигается вдоль поверхности

Земли, не касаясь ее, значит, реакция опоры (сила

упругости) N = 0, и на тело в этом случае действу-

ет единственная сила – сила тяготения (сопротив-

ление воздуха не учитываем). Поскольку тело движется по окружности, то, согласно

второму закону Ньютона, произведение массы m тела на центростремительное ус-

корение равно силе тяготения (см. рисунок 4):

m

З

R

v = mg, (5.17)

откуда получаем

v1 = gRЗ = 6 4 10 м

с

9 81 м 6

2, ,  = 7,91106 м/с  7,9 км/с. (5.18)

Так как согласно (5.3) g = G 2

З

З

R

M, то из (5.18) можем получить ещё одно выражение

для v1:

v1 = З gR = 2 З

З

З R

R

G M =

З

З

R

GM. (5.19)

Для разных планет их массы М и радиусы R различные, поэтому первые

космические скорости v1 для разных планет различные.

Рисунок 4

v 1

N

m g

R З

На спутник, движущийся по круговой орбите радиусом r (r = R + h, R – радиус

планеты, h – высота над поверхностью планеты), действует сила тяготения, сооб-

щающая ему нормальное ускорение v2/r. Из второго закона Ньютона с учётом выра-

жения (5.5)

m

r

v2

= mg(h) = mg  2

R h

R



= mg

r

R







 (5.20)

находим первую космическую скорость для спутника, движущегося по круговой ор-

бите радиуса r:

v = R

r

g. (5.21)

Период обращения спутника Т = 2/, v = r. С учётом выражения (5.21) для v,

получим

T = 2

3 2 1 2

g

R

R

r / /

 



 









. (5.22)

Полагая радиус орбиты спутника равным радиусу планеты, т.е. r = R, получим наи-

меньшее значение периода обращения

Т = 2

1/ 2

g

R

 



 



. (5.23)

Так как согласно (5.22) Т  r3/2, то отсюда следует, что отношение квадратов пе-

риодов вращения двух спутников равно кубу отношения радиусов круговых орбит:

Т

Т

 



 



=

r

r

 



 



или 3

r

Т =  

GM

2 2 

. (5.24)

Первой космической скорости недостаточно для того, чтобы тело могло выйти

из сферы земного притяжения, т.е. удалилось на такое расстояние, при котором при-

тяжение к Земле становится пренебрежимо малым. Необходимая для этого скорость

называется второй космической скоростью v2. Расчёты дают, что вторая космиче-

ская скорость в 2 раз больше первой космической скорости v1, т.е.

v2 =

R

2GM = 2gR = v1 2, (5.25)

где М – масса планеты,

R – ее радиус.

Date: 2015-08-15; view: 504; Нарушение авторских прав