Теорема про змiну моменту кiлькостi руху матерiальної системи

Повна похiдна за часом від вектора момента кiлькостi руху матерiальної системи вiдносно нерухомого центру О дорiвнює сумi моментiв всiх зовнiшнiх сил вiдносно того ж центру:

(13.22)

Моментом кiлькостi руху (кiнетичним моментом) матерiальної системи вiдносно центру О називається сума моментiв кiлькостей руху всiх матерiальних точок, що входять до складу системи, вiдносно того ж центра:

(13.23)

де 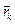- радiус-вектор матерiальної точки маси m_k з початком в центрi О; m_k - маса k -тої точки; 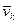- швидкiсть k -тої матерiальної точки. Якщо матерiальна система являє собою безперервно розподiлене матерiальне середовище, що заповнює деякий об’єм, то сума перейде у вiдповiдний iнтеграл.

В проекцiях на нерухомi осi декартових координат, початок яких спiвпадає з центром О, векторне рiвняння (13.22) еквiвалентне трьом скалярним:

(13.24)

де K_x, K_y, K_z – проекції вектора 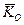на координатнi вiсi з початком в центрi О, якi можна визначити за формулами:

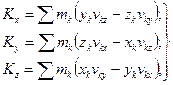(13.25)

де x_k, y_k, z_k - координати точки маси m_k.

Момент кiлькостi руху твердого тiла при обертаннi навколо нерухомої осi дорiвнює добутку моменту iнерцiї тiла вiдносно цiєї ж осi та проекцiї кутової швидкостi тiла на цю вiсь:

K_z = I_zω_z. (13.26)

У випадку сферичного руху твердого тiла

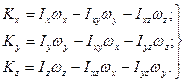(13.27)

Якщо осi координат, що мають початок в нерухомiй точцi О тiла, будуть головними осями iнерцiї, то

I_xy = I_xz = I_yz = 0

i з (13.27) одержимо

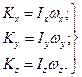(13.28)

Формули (13.28) визначають проекцiї моменту кiлькостi руху твердого тiла, що має одну нерухому точку, на осi координат, незмiнно пов’язанi з тiлом. З цих формул видно, що в загальному випадку проекцiї вектора 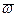i проекцiї вектора 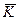не пропорцiйнi мiж собою, а тому напрям векторiв 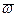i 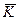не спiвпадає.

При русi тiла навколо нерухомої осi за умови, що вона спiвпадає з вiссю обертання тiла, маємо

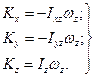(13.29)

Якщо матерiальна система здiйснює складний рух, то момент кiлькостi абсолютного руху 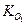вiдносно нерухомого центра О ₁ дорiвнює сумi моменту кiлькостi руху центра мас системи вiдносно О ₁ в припущеннi, що в ньому зосереджена вся маса системи, i моменту кiлькостi вiдносного руху вiдносно центра мас:

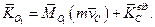(13.30)

В проекцiях на декартовi осi координат

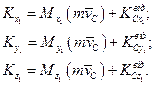(13.31)

Теорема про змiну кiнетичного моменту матерiальної системи має такi наслiдки:

а) внутрiшнi сили безпосередньо не впливають на змiну моменту кiлькостi руху матерiальної системи. Внутрiшнi сили можуть мати вплив на рух системи через зовнiшнi сили;

б) якщо головний момент всiх зовнiшнiх сил вiдносно деякого нерухомого центру дорiвнює нулю, то момент кiлькостi руху матерiальної системи вiдносно того ж центру не змiнюється за модулем i напрямом:

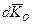( /dt) = 0, K_O = const;

в) якщо головний момент всiх зовнiшнiх сил вiдносно нерухомої осi (наприклад, осi х) дорiвнює нулю, то момент кiлькостi руху матерiальної системи не змiнюється в процесi руху:

(dК_x/dt) = 0, K_x = const.

При розв’язаннi задач з використанням теореми про змiну моменту кiлькостi руху матерiальної системи необхiдно дотримуватись такої послiдовностi:

1) вибрати координатнi осi, направити одну з осей вздовж нерухомої осi обертання;

2) показати на рисунку всi зовнiшнi сили системи;

3) записати теорему про змiну головного моменту кiлькостi руху матерiальної системи вiдносно вибраної осi, наприклад

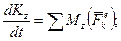
4) обчислити суму моментiв зовнiшнiх сил вiдносно осi z;

5) обчислити кiнетичний момент системи вiдносно нерухомої осi;

6) скласти рiвняння теореми про змiну кiнетичного моменту системи;

7) обчислити шуканi величини.

Зауваження. Для закріплення матеріалу §13 (пункт 13.6) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 37.1 - 37.5, 37.50, 37.52, 37.56;

2) № 37.6, 37.7, 39.9, 37.11, 37.43 – 37.48, 37.53;

3) № 37.57 - 37.59.

Рекомендується розв’язати також задачі № 9.18, 9.19, 9.21, 9.24 - 9.28, 9.38, 9.39, 9.43 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Date: 2015-08-15; view: 353; Нарушение авторских прав