Теорема про зміну кінетичної енергії матеріальної системи

Зміна кінетичної енергії матеріальної системи при її переході з початкового в кінцеве положення дорівнює сумі робот всіх зовнішніх та внутрішніх сил, прикладених до точок системи, на цьому переміщенні:

Т- Т ₀ = А^е + А^і, (13.32)

де Т ₀ - початкове значення кінетичної енергії, Т - кінцеве значення кінетичної енергії, А^е і А^і - роботи всіх зовнішніх і внутрішніх сил системи.

Продиференціюємо рівність (13.32) за часом:

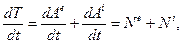(13.33)

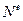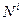де і - потужності зовнішніх і внутрішніх сил системи.

Рівність (13.33) є аналітичним записом теореми про зміну кінетичної енергії системи в диференціальній формі: повна похідна від кінетичної енергії за часом дорівнює сумі потужностей всіх зовнішніх і внутрішніх сил, прикладених до системи.

За допомогою теореми про зміну кінетичної енергії в інтегральній формі визначають:

1) швидкості точок матеріальної системи;

2) роботу однієї з сил, прикладених до системи, коли з умови задачі швидкості точок матеріальної системи відомі або їх можна визначити іншими методами.

Диференціальна форма теореми про зміну кінетичної енергії системи матеріальних точок застосовується для складання диференціальних рівнянь руху, а також для визначення лінійних або кутових прискорень.

Кінетична енергія матеріальної системи дорівнює сумі кінетичних енергій всіх матеріальних точок:

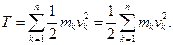(13.34)

Кінетична енергія твердого тіла обчислюється за формулами:

а) при поступальному русі

(13.35)

б) при обертанні твердого тіла навколо нерухомої осі

(13.36)

де І_z - момент інерції твердого тіла відносно осі обертання z, ω - кутова швидкість обертання;

в) при плоскому русі

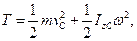(13.37)

де v_C - швидкість центра мас тіла, І_zC - момент інерції тіла відносно осі z, що проходить через центр мас перпендикулярно до площини руху, ω - величина миттєвої кутової швидкості твердого тіла. В цьому випадку обчислення кінетичної енергії можна робити також за формулою

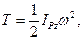(13.38)

де І_Pz - момент інерції твердого тіла відносно осі z, що проходить через миттєвий центр швидкостей перпендикулярно до площини руху;

г) при обертанні навколо нерухомої точки (при сферичному русі)

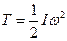, (13.39)

де І - момент інерції тіла відносно миттєвої осі обертання, ω - модуль миттєвої кутової швидкості.

Якщо вибрати початок рухомих осей х, у, z, пов’язаних з твердим тілом, в нерухомій точці О, то

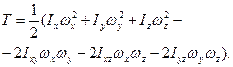(13.40)

Якщо х, у, z є головними осями інерції твердого тіла в нерухомій точці О, то І_ху=І_xz=І_yz= 0, і значить

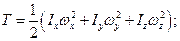(13.41)

д) в загальному випадку руху твердого тіла

(13.42)

де v_C - модуль швидкості центра мас, І_C - момент інерції відносно миттєвої осі, що проходить через центр мас, ω - модуль миттєвої кутової швидкості.

Якщо вибрати початок рухомих координатних осей х, у, z в центрі мас, то

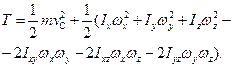(13.43)

Якщо осі х, у, z є головними центральними осями інерції в центрі мас С, то І_ху=І_xz=І_yz= 0, і значить

(13.44)

Теорема Кеніга: кінетична енергія механічної системи при довільному русі дорівнює сумі кінетичної енергії центра мас в припущенні, що в ньому зосереджена маса всієї системи, і кінетичної енергії системи в її русі по відношенню до центра мас:

(13.45)

де 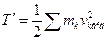- кінетична енергія системи в її русі відносно центру мас, v_kвід - швидкість k -тої точки системи по відношенню до рухомих осей координат.

Розв’язання задачі за допомогою теореми про зміну кінетичної енергії можна проводити в такій послідовності:

1) показати на рисунку всі зовнішні і внутрішні сили системи. Якщо система незмінювана, то треба показувати тільки зовнішні сили;

2) обчислити суму робот всіх зовнішніх і внутрішніх сил на переміщеннях точок системи. Якщо система незмінювана, то потрібно обчислити тільки роботу зовнішніх сил;

3) обчислити кінетичну енергію системи в початковому і кінцевому положеннях системи;

4) записати теорему про зміну кінетичної енергії системи матеріальних точок:

,

для незмінюваної системи ;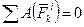

5) визначити шукану величину.

Зауваження. Для закріплення матеріалу §13 (пункт 13.7) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 38.1, 38.3, 38.4, 38.7 - 38.10, 38.11, 38.13, 38.14, 38.20, 38.21, 38.27;

2) № 38.16 - 38.18, 38.23, 38.24, 38.27, 38.28, 38.30 – 38.33, 38.35, 38.36, 38.38, 38.40, 38.44;

3) № 38.42, 38.43, 38.46, 38.47, 38.50, 38.51 - 38.53.

Рекомендується розв’язати також задачі № 9.46, 9.47, 9.49, 9.50, 9.52, 9.53, 9.55, 9.57 – 9.59, 9.63 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Date: 2015-08-15; view: 450; Нарушение авторских прав