Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Колебание опорных конструкций и элементов
|
|
Представим некоторую опорную конструкцию в виде балки, на которой расположена машина (механизм) массой m, к которой прикладывается возмущающая сила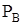 
(рис. 29).
 |
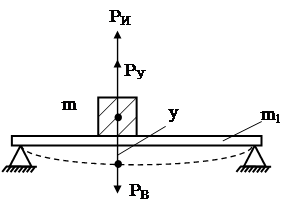Рис. 29. Расчетная схема
При динамическом нагружении балки будут действовать силы:
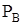– возмущающая сила;
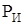– сила инерции системы;
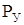– сила упругости балки.
Динамическое условие равновесия
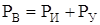. (220)
В свою очередь
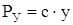, (221)
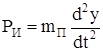, (222)
где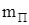 
– приведенная масса механизма m и балки 
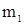в точке приложения .
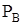Тогда
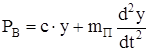, (223)
или
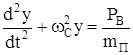, (224)
где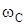 
– собственная частота колебаний системы.
Поведение системы зависит от характера изменения возмущающей силы. Рассмотрим случай, когда источником возмущающей силы является центробежная сила PЦ от неуравновешенной массы механизма (муфта, несимметричная деталь и т.п.). Схема этого случая проиллюстрирована рис. 30 и 31.
 |
Согласно рис. 30 и 31, деформацию y при колебаниях балки будет определять вертикальная составляющая возмущающей силы
.
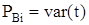Тогда
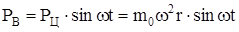, (225)
где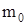 
– смещенная масса;
r – радиус вращения смещенной массы .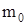
С учетом этого уравнение (224) примет вид
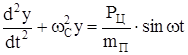. (226)
В результате решения уравнения (226) получим
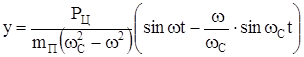. (227)
Анализ показывает, это второй член уравнения (227) в скобках учитывает вынужденные колебания системы с собственной частотой wС, которые при установившемся движении затухают и ими можно пренебречь.
Тогда
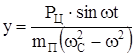. (228)
Максимальная деформация при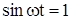 
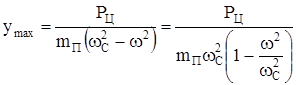. (229)
Поскольку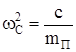 
, будем иметь
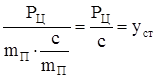, (230)
или
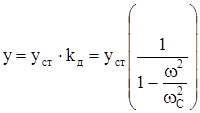. (231)
Анализ формулы (231) показывает, что при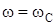 
наступает явление резонанса, характеризующееся тенденцией 
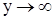. Однако изложенный выше вывод не учитывает сопротивлений в системе.
При учете сопротивлений (вязкое трение в металле, трение в соединениях и другие потери) динамическое уравнение будет включать еще силу сопротивления, которая, согласно Фойгту, прямо пропорциональна скорости движения
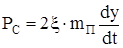, (232)
где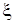 
– коэффициент, пропорциональный собственной частоте колебаний системы.
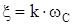. (233)
Для стальных конструкций k=0,02…0,08.
С учетом сопротивлений дифференциальное уравнение будет иметь вид
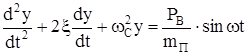. (234)
В результате решения уравнения (234) получим
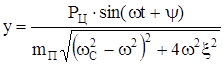, (235)
где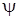 
– фазовый угол (разность фаз), отражающий запаздывание перемещения по отношению к возмущающей силе.
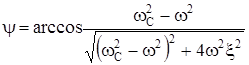. (236)
Максимальное перемещение (деформация) будет при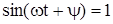 
:
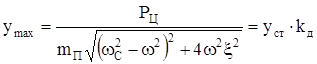, (237)
где коэффициент динамичности kд равен
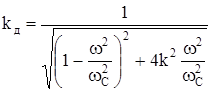. (238)
Для условия резонанса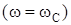 
имеем
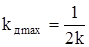. (239)
Для стальных конструкций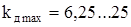 
.
Date: 2015-08-15; view: 365; Нарушение авторских прав