Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Задача ДС.3. Застосування теореми про зміну моменту імпульсу для визначення кутової швидкості механічної системи
|
|
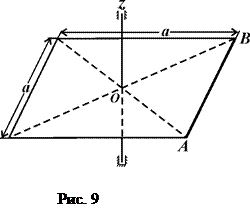
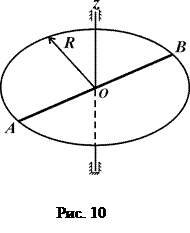
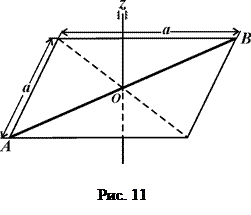
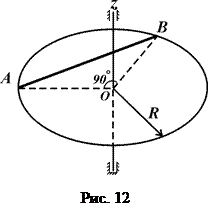
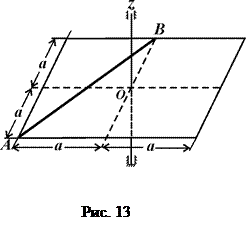
Тіло масою 
кг (рис. 8 – 13) обертається навколо фіксованої осі 
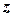, яка проходить через його центр перпендикулярно до його площини з початковою кутовою швидкістю 
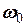рад/с. В точці 
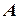в стані спокою знаходиться механізм масою 
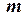кг. В момент часу 
= 0 починає діяти момент зовнішніх сил 
. Визначити кутову швидкість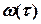 
обертання тіла в момент часу 
.
Далі тіло обертається по інерції з досягнутим значенням кутової швидкості. В деякий новий момент часу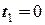 
самохідний механізм починає рухатись за законом 
вздовж траєкторії 
(
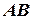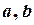- сталі величини; відстань в метрах, час в секундах). Вважаючи механізм матеріальною точкою, знайти кутову швидкість диску як функцію часу 
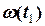та підрахувати її значення на момент часу 
= 
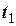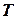с.
Таблиця 3
Вихідні дані для задачі ДС.3
| № | рис. |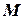 
| 
| 
| 
|
|
| 
| 
|
|
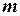
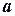
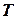
- 720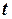 
| -1 | - 2 | ||||||||
- 240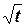 
| 1,5 | 0,5 | ||||||||
| 1,5 | 375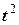 
| |||||||||
| 720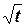
| - 1 | |||||||||
-400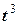 
| 
| |||||||||
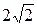
| 450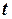
| 
| |||||||||
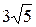
| 135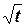
| - 3 | - 2 | ||||||||
| - 625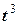
| ||||||||||
| - 510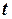
| - 2 | |||||||||
| 420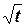
| ||||||||||
| 135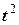
| 
| |||||||||
| - 640
| 
| |||||||||
| - 300
| - 1 | |||||||||
| 400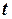
| 0,5 | |||||||||
| 4,5 | - 375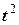
| - 0,5 | ||||||||
| -625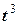
| ||||||||||
| 420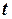
| 
| |||||||||
| - 270
|
| |||||||||
| 400
| - 2 | - 1 | ||||||||
| - 360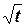
| ||||||||||
| - 135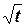
| ||||||||||
| 800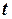
| - 2 | 3,5 | ||||||||
| - 720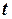
| 
| |||||||||
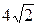
| - 400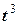
|
| |||||||||
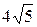
| 135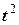
| ||||||||||
| 875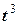
| - 0,5 | |||||||||
| - 510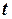
| - 1 | |||||||||
| 240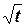
| - 2 | |||||||||
| -420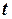
|
| |||||||||
| 405
|
|
| 
|
| 
|
| 
|
Приклад 1. Однорідний диск масою = 400 кг і радіуса 
= 5 м обертається навколо фіксованої осі, яка проходить через його центр перпендикулярно до його площини з початковою кутовою швидкістю 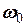= 4 рад/с (рис. 14). На відстані 
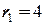м від осі обертання в стані спокою знаходиться механізм масою 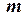=150 кг. В момент часу = 0 починає діяти момент зовнішніх сил 
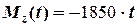. Визначити кутову швидкість 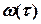обертання тіла в момент часу 
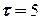с.
Далі тіло обертається за інерцією з досягнутим значенням кутової швидкості. В деякий новий момент часу 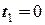самохідний механізм перемістіться на відстань 
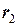= 2 м від центру диску та повністю загальмується. Вважаючи механізм матеріальною точкою, знайти кутову швидкість диску на цей момент.
Розв’язок. Для розв’язку задачі скористаємося теоремою про зміну моменту імпульсу механічної системи
,
де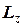 
- момент імпульсу системи відносно осі 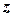, який складається з диска та механізму; 
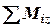- головний момент зовнішніх сил, прикладений до системи, відносно осі .
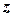Розглянемо схему руху механічної системи, сумістивши вісь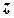 
системи відліку з віссю обертання диску та позначимо сили, які діють на систему - це сили тяжіння 
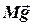та 
, пара сил з моментом та реакцій підп’ятника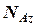 
та підшипника 
. Обидві сили тяжіння спрямовані паралельно осі обертання і, відповідно, їхні моменти відносно цієї осі дорівнюють нулю; не створюють моменту і сили реакції, бо проходять через вісь 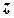. Отже, головний момент зовнішніх сил дорівнює моменту .
Момент імпульсу системи є сумою кінетичних моментів її елементів. Момент імпульсу твердого тіла (диску), яке має певний момент інерції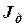 
відносно осі 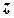та обертається навколо неї з кутовою швидкістю 
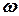, визначається як
,
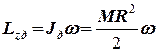а момент імпульсу матеріальної точки, згідно з визначенням
,
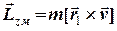де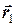 
- радіус-вектор, який проведено від осі обертання до точки, а 
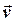- абсолютна швидкість точки. Абсолютну швидкість точки, яка не рухається по диску, але обертається разом з диском навколо фіксованої осі з кутовою швидкістю 
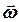, визначити за формулою Ейлера
,
отже
.
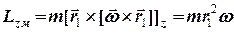Таким чином момент імпульсу системи
,
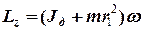а рівняння про зміну моменту імпульсу приймає вид
.
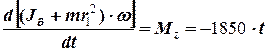Розділимо змінні та про інтегруємо праву та ліву частини рівняння
,
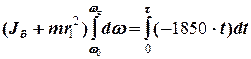та отримуємо
.
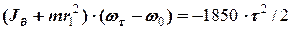Підставляючи чисельні значення, знаходимо
(рад/c).
Після того, як перестав діяти момент зовнішніх сил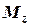 
диск обертається за інерцією. Така ситуація дає можливість скористатись теоремою про збереження моменту імпульсу відносно цієї осі
,
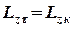де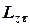 
та 
- відповідно 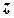- компоненти початкового і кінцевого моменту імпульсу системи. Прирівнюючи відповідні вирази маємо
= 
,
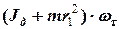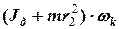що дозволяє отримати вираз для розрахунку кінцевої кутової швидкості обертання диску
.
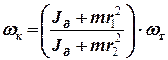Підставляючи чисельні значення, отримуємо
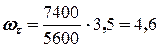(рад/c).
Відповідь: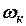 
= 4,6 рад/с.
Приклад 2. Диск масою = 300 кг і радіуса = 8 м обертається навколо фіксованої осі, яка проходить через його центр перпендикулярно до його площини з кутовою швидкістю 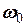= 5 рад/с (рис. 15). На відстані 
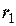= 7 м від центру 
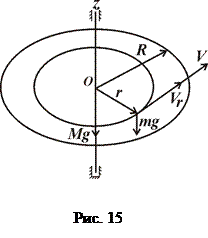диску в стані спокою знаходиться механізм масою 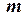=100 кг. В момент часу = 0 механізм починає рухатись вздовж кола незмінного радіуса за законом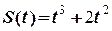 
в напрямі обертання диску (відстань в метрах, час в секундах). Вважаючи механізм матеріальною точкою, знайти кутову швидкість диску як функцію часу 
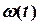та її значення на момент часу 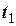= 2 с.
Розв’язок. Як і у попередньому випадку, легко бачити, що моменти зовнішніх сил відносно осі обертання 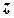дорівнюють нулю, що дає можливість скористатись теоремою про збереження моменту імпульсу відносно цієї осі
,
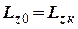де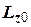 
та початковий і кінцевий моменти імпульсу системи відповідно.
Момент імпульсу твердого тіла (диску), момент інерції якого 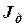відносно осі 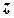та який обертається навколо неї з кутовою швидкістю 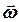, відомий, тому
.
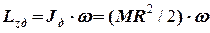Момент імпульсу матеріальної точки, згідно з визначенням:
,
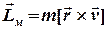де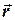 
- радіус-вектор, який проведено від осі обертання до точки, а 
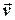- абсолютна швидкість точки. На відміну від попереднього прикладу, тепер абсолютна швидкість точки складається зі швидкості відносного руху точки 
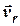та переносної швидкості 
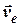, яку має будь-яка точка диску завдяки обертанню диска з кутовою швидкістю 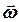, яку знаходимо за теоремою про швидкість складного руху
,
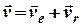тому
.
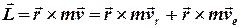Швидкість переносної руху точки у довільний момент часу
,
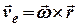а модуль відносної швидкості визначимо як першу похідну відносного переміщення точки за часом
.
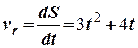Оскільки ця швидкість спрямована по дотичній до кола радіуса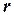 
, тому з врахуванням напряму руху точки та обертання диску для абсолютної швидкості точки отримуємо
.
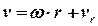Підставляючи отриманий вираз, знаходимо вираз для кінцевого значення моменту імпульсу точки
.
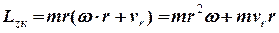Скористуємось тим, що напрями початкової кутової швидкості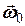 
та осі 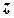співпадають, і запишемо початковий момент імпульсу системи в вигляді
.
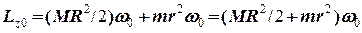Запишемо вираз для кінцевого значення моменту імпульсу системи, вважаючи, що напрям обертання не змінився. Тоді
,
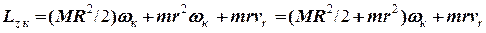де 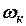- кінцева кутова швидкість обертання диску.
Прирівнявши вирази які визначають закон збереження 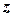- компоненти моменту імпульсу механічної системи отримуємо вираз для розрахунку кінцевої кутової швидкості диску
.
Підставимо дані задачі та отримаємо значення для кінцевої кутової швидкості диску:
= 3,6 (рад/с).
Відповідь: 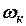= 3,6 рад/с.
Самостійно проаналізуйте задачу, коли відносна швидкість механізму протилежна переносній швидкості точок диска, де він знаходиться.
Date: 2015-08-15; view: 606; Нарушение авторских прав