Задача ДС.2. Застосування теореми про зміну імпульсу для дослідження руху механічної системи

Непарні варіанти: Човен масою М кг рухається зі швидкістю V ₀ м/с. У певний момент часу курсанти, маси яких 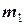кг та кг відповідно, стрибають одночасно з човна зі швидкостями та м/с відносно човна. Перший курсантів стрибає під кутом °, а другий - під кутом 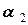° до горизонту (рис. 4). Знайти кінцеву швидкість човна. Додатний напрям стрибка співпадає з початковим напрямом руху човна. Силами тертя нехтувати та не враховувати вертикальні коливання човна.

Парні варіанти: По порому масою 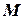, який має швидкістю м/с рухається автомобіль масою 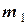зі швидкістю м/с відносно порому (рис. 5). Автомобіль починає змінювати швидкість. Знайти швидкість порому на момент, коли відносна швидкість автомобілю становить м/с. Опором повітря та води нехтувати. (Знаки швидкостей та вказані по відношенню до швидкості платформи ).

Таблиця 2

Вихідні дані для задачі ДС.2

№	M		m 1	V 1	°	напрям	m 2	V 2	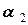°	напрям
		4,0		7,0		-		2,0		+
		3,0		- 5,0	---	---	---	1,5	---	---
		6,5		4,5		-		1,0		-
		3,5		4,0	---	---	---	- 1,5	---	---
		4,0		7,0		+		3,5		+
		5,5		4,5	---	---	---	1,5	---	---
		4,5		6,0		+		1,0		-
		4,5		- 4,0	---	---	---	- 1,0	---	---
		5,0		5,0		-		3,5		-
		4,0		3,0	---	---	---	- 1,5	---	---
		3,0		5,0		-		1,5		-
		4,5		1,0	---	---	---	4,0	---	---
		6,5		6,5		-		3,0		-
		3,0		- 1,5	---	---	---	4,0	---	---
		4,5		5,0		-		3,5		-
		4,5		1,0	---	---	---	4,5	---	---
		6,5		5,0		-		3,5		-
		5,5		- 4,5	---	---	---	- 1,0	---	---
		6,5		4,0		+		1,5		+
		4,0		3,5	---	---	---	1,0	---	---
		5,5		5,0		-		1,5		+
		5,0		- 1,5	---	---	---	3,0	---	---
		5,5		6,5		-		3,5		-
		4,5		1,0	---	---	---	4,0	---	---
		6,0		5,5		-		2,5		-
		4.5		3,0	---	---	---	- 1,5	---	---
		7,0		6,0		-		2,5		-
		3,5		- 1,0	---	---	---	- 4,5	---	---
		4,0		4,0		-		2,0		-
		5,0		4,0	---	---	---	0 1,0	---	---

Приклад 1. Човен масою М = 200 кг на якому знаходиться курсант масою 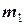= 70 кг рухається зі швидкістю
V ₀ = 2 м/с. У певний момент часу курсант стрибає з човна зі швидкістю = 5 м/с відносно човна під кутом 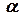= 60° до горизонту (рис. 6). Знайти кінцеву швидкість човна. Силами тертя нехтувати.

Розв’язок. Перш за все, виберемо систему відліку, зв’язавши її з яким-небудь нерухомим об’єктом (деревом на березі) та спрямуємо вісь 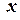вздовж напряму руху човна. Оскільки ми нехтуємо силами тертя, то вздовж напряму руху зовнішні сили відсутні і ми можемо скористуватись теоремою про збереження компоненти імпульсу

,

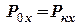де та 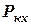початковий та кінцевий імпульси системи відповідно. Оскільки в початковий момент курсант знаходяться у стані спокою відносно човна то початковий імпульс можна записати як

.

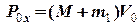Вертикальна складова імпульсу курсанта зумовлює додаткове занурення човна, яке в даному випадку нас не цікавить. Щоб записати 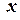- компоненту кінцевого імпульсу системи, який вона набуває в момент відштовхування курсанта від човна, будемо вважати, що напрям руху човна не змінюється, а його швидкість дорівнює 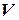. Тоді компонента абсолютної швидкості курсанта вздовж осі 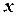буде 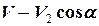, тому

.

Прирівнюючи кінцевий та початковий імпульси, отримаємо

= ,

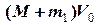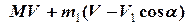що дозволяє визначити кінцеву швидкість човна

.

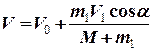Підставимо умови задачі в отриманий вираз та знайдемо

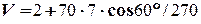= 2,9 (м/с).

Відповідь: = 2,9 м/с.

Проаналізуйте самостійно кінцеву формулу для випадків: а) 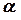=0°; б) 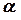= 90°.

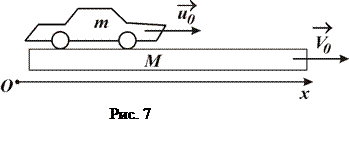Приклад 2. По порому 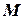=3т, який пливе зі швидкістю 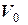=6 м/с рухається автомобіль масою 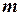= 1,5 т зі швидкістю 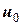= 2 м/с відносно порому (рис. 7). Автомобіль починає гальмувати. Знайти швидкість порому на момент, коли відносна швидкість автомобілю становить 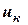= 0,5 м/с. Опором повітря та води нехтувати.

Розв’язок. Як і у попередньому прикладі, виберемо систему відліку, зв’язавши її з яким-небудь нерухомим об’єктом (маяком на березі) та спрямуємо вісь 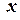вздовж напряму руху порому. Оскільки ми нехтуємо силами тертя, то вздовж напряму руху зовнішні сили відсутні і ми можемо скористуватись теоремою про збереження імпульсу

,

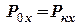де та 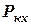початковий та кінцевий імпульси системи відповідно. Оскільки в початковий момент автомобіль рухається в напрямі руху порому, його абсолютна швидкість дорівнює 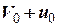і початковий імпульс системи відносно обраної системи відліку можна записати як

.

Щоб записати кінцевий імпульс системи, будьмо вважати, що напрям руху порому не змінюється, а його швидкість дорівнює 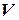. Тоді абсолютна швидкість автомобіля вздовж осі 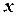буде 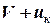, і кінцевий імпульс системи відносно нерухомої системи відліку

.

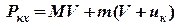Прирівнюючи кінцевий та початковий імпульси, отримаємо

= ,

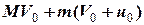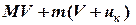що дозволяє визначити кінцеву швидкість порома

.

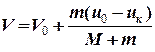Підставимо умови задачі та знайдемо

= 6,5 (м/с).

Відповідь: = 6,5 м/с.