Задача ДС.1. Дослідження руху центру мас механічної системи

Непарні варіанти: Тіло 3 з закріпленим на ньому електродвигуном (загальна маса тіла та двигуна М кг) може ковзати вздовж горизонтальної поверхні без тертя (рис. 1). На співосних валах електродвигуна, на відстанях та 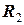від осі обертання, жорстко закріплені тіла, масами m₁ та m₂ кг відповідно, розмірами яких можна нехтувати. В початковий момент часу система знаходиться у стані спокою, а тіла m₁ та m₂ знаходяться в початкових точках А і В відповідно таблиці 1. В момент часу t ₀ = 0 вали починають обертатися за певними законами 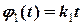рад та рад.

1. Знайти закон зміщення тіла 3 від часу.

2. Знайти реакцію упорів, які утримують тіло 3 в закріпленому стані.

(Додатному напряму обертання відповідає обертання проти стрілки годинника.)

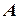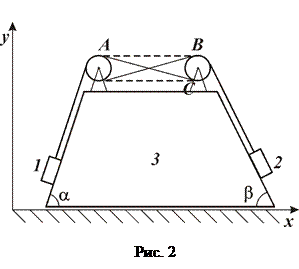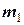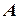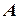Парні варіанти: Призма 3 з закріпленим на ньому електродвигуном та блоком (загальна маса М кг) може ковзати вздовж горизонтальної поверхні без тертя (рис. 2). Два вантажі, маса яких та ковзають по гладким поверхням призми, які утворюють кути та з горизонтом, бо з’єднані мотузками з двигуном та блоком . Електродвигун , радіус якого , зв’язаний з блоком , радіус якого 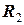, пасовою передачею перехресною (з’єднання 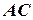), або прямою (з’єднання 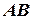). В момент часу t ₀ = 0 електродвигун починає обертатися за законом рад. Вагою мотузок та пасу нехтуючи і вважати їх нерозтяжними.

1. Знайти закон зміщення призми від часу.

2. Знайти реакцію упорів, які утримують призму в закріпленому стані.

(Додатному напряму обертання відповідає обертання проти стрілки годинника.)

Таблиця 1

Вихідні дані для задачі ДС.1

№	M	m 1 (двигун A)	m 2
маса	R 1	Початкове положення	Напрям Обертання	маса	R 2	Початкове положення	Напрям обертання	k 1	k 2			тип
			0,40	A1	-		0,30	B2	-
			0,20		+		0,30							AB
			0,70	B1	-		0,15	B2	+
			0,15		-		0,25							AC
			0,45	D1	-		0,25	E2	+
			0,25		+		0,15				- 2			AB
			0,70	E1	-		0,25	D2	-
			0,40		-		0,20				- 1			AC
			0,50	B1	+		0,15	B2	+
			0,20		+		0,40							AB
			0,45	D1	-		0,35	B2	+
			0,25		-		0,50				- 2			AC
			0,40	B1	-		0,30	A2	-
			0,50		+		0,25							AB
			0,55	A1	-		0,20	D2	+
			0,20		-		0,30				- 3			AC
			0,55	B1	-		0,20	B2	-
			0,30		+		0,20							AB
			0,50	D1	-		0,10	D2	+
			0,45		-		0,15				- 1			AC
			0,60	E1	+		0,20	D2	-
			0,15		+		0,45				- 2			AB
			0,70	A1	-		0,25	B2	+
			0,15		-		0,05							AC
			0,55	B1	+		0,10	B2	+
			0,05		+		0,15				- 2			AB
			0,60	A1	+		0,10	D2	-
			0,10		-		0,20							AC
			0,60	D1	-		0,10	B2	+
			0,20		+		0,10				- 3			AB

Приклад. Тіло G з закріпленим на ньому електродвигуном (загальна маса тіла та двигуна М = 150 кг) може ковзати вздовж горизонтальної поверхні без тертя. На співосних валах електродвигуна, на відстанях R₁ = 0,5 м та R₂ = 0,2 м від осі обертання, жорстко закріплені тіла, розмірами яких можна нехтувати, масами m₁ = 20 кг та m₂ = 30 кг, відповідно. В початковий момент часу система знаходиться у стані спокою, а тіла m₁ та m₂ знаходяться в точках А і В, відповідно (рис. 3). 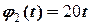В момент часу t ₀ = 0 вали починають обертатися за стрілкою годинника за законами рад/с та рад/с.

1. Знайти закон зміщення тіла G від часу.

2. Знайти реакцію упорів, які утримують тіло G в закріпленому стані.

Розв’язок. Перш за все, довільно оберемо систему відліку (дивись рис. 3) спрямувавши вісь 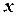горизонтально. Згідно з теоремою про рух центру мас механічної системи у відсутності зовнішніх сил прискорення центру мас системи дорівнює нулю. Для нашого випадку вздовж горизонталі зовнішні сили відсутні і в початковий момент часу система знаходиться у спокою, отже положення центру мас системи вздовж осі 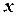не змінюється. Математично це можна записати наступним чином

, (1)

тут 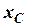- координата центру мас системи, 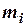- маса елемента системи, 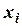- координата центру його маси. На момент часу 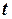= 0 отримане рівняння можна записати у вигляді

,

де 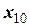, 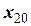та 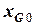- початкові координати елементів системи, а для будь-якого моменту часу

,

де 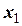, 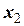та 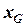- координати елементів на момент часу 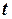≠ 0.

Зв’язок між початковими та поточними координатами легко знайти наступним шляхом. Будемо вважати, що за досить малий інтервал часу 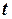тіло G змістилося вправо на відстань 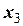відносно початкового положення. Тоді абсолютні координати тіл, що обертаються, є алгебраїчними сумами зміщення тіла G та відповідних відносних зміщень AD і CE тіл 1 і 2 вздовж осі x відповідно (рис. 3). Ці відносні зміщення можна знайти з геометричних міркувань:

,

.

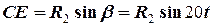Таким чином, зв’язок між відповідними координатами наступний:

.

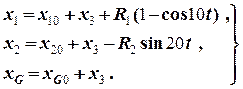Незмінність координати центру маси системи (1) дає

.

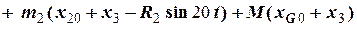Якщо розкрити дужки та провести алгебраїчні перетворення, то дістаємо

.

Отриманий вираз дає зміщення тіла G в будь-який момент часу. Підставляючи числа в цей вираз, отримаємо зміщення на заданий момент часу

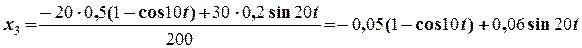(м).

Для відповіді на друге запитання перепишемо закон руху центру мас механічної системи у вигляді

,

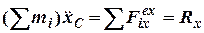де 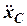- друга похідна зміщення центра мас за часом (прискорення), - сума зовнішніх сил, що діють на систему в горизонтальному напрямку, яка визначає реакцію упору . З урахуванням виразу для 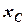маємо

.

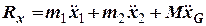При наявності упорів тіло G не рухається, отже 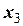= 0 і 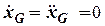. Оскільки 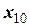, 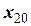та 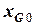- величини сталі, то послідовно отримаємо

,

та для реакції упору

=

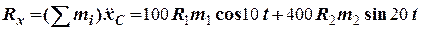= = (Н).

Відповідь: 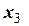= 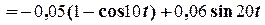м,

= Н.

Date: 2015-08-15; view: 459; Нарушение авторских прав