Б) Вільні згасаючі коливання з одним ступенем свободи

Розглянемо одномірний рух тіла вздовж вісі 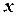у в’язкому середовищі (рідині або газі). При незначних швидкостях руху тіла сила опору пропорційна швидкості, тобто

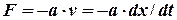. (1)

Тоді диференціальне рівняння руху буде мати вигляд

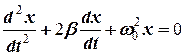, (2)

де

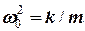. (3)

Зауважимо, що розмірності та однакові (с ^-1), що дозволяє порівнювати їх між собою. Отримане диференціальне рівняння другого порядку має таке характеристичне рівняння

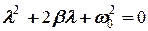, (4)

корені якого будуть

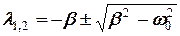. (5)

Співвідношення між та визначають характер руху тіла. Розглянемо випадок < , який відповідає незначним силам тертя в порівнянні з середнім значенням пружної сили. Тоді корені характеристичного рівняння будуть комплексними

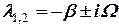, (6)

де

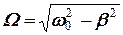, (7)

і загальний розв’язок рівняння (2) буде мати вигляд

. (8)

Початкові амплітуда та фаза 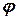визначаються початковими умовами, і ми у змозі знайти їх шляхом, який аналогічний тому, яким ми користувались для вільних незатухаючих коливань.

Коливання, що відбуваються за законом (8) називаються затухаючими (загасаючими), бо присутність коефіцієнта при амплітуді коливань зумовлює поступове зменшення відхилення тіла від положення рівноваги, та, з часом, і до зникнення коливань. Отже рух точки можна розглядати як гармонічне коливання з частотою 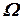та амплітудою, яка змінюється за законом

. (9)

Відношення послідовних амплітуд (за період коливань ) можна записати як:

. (10)

Таким чином, послідовні відхилення створюють геометричну прогресію зі знаменником , який називається декрементом затухань, а величина

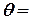
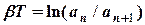(11)

називається логарифмічним декрементом затухань.

В випадку 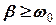коливання становляться аперіодичними.

Контрольні запитання

1. Сформулюйте умови виникнення загасаючих коливань.

2. Запишіть диференціальне рівняння вільних загасаючих коливань. Що необхідно знати для однозначного розв’язку такого рівняння?

3. Як отримати розв’язок такого рівняння?

4. Запишіть розв’язок диференціального рівняння вільних загасаючих коливань.

5. Що таке амплітуда коливань? Від чого вона залежить? За яким законом змінюється амплітуда коливань?

6. Від чого залежить період (частота) коливань? Як впливає сили тертя на частоту (період) коливань?

7. Що визначає декремент затухання?

8. Коли виникають аперіодичні коливання? Яке застосування таких процесів Ви знаєте?

Приклад. Знайти рівняння коливань тіла масою 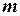= 0,6 кг, яке закріплено до двох послідовно скріплених пружин жорсткістю = 150 Н/м та
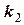=100 Н/м (рис. 8), якщо сила опору 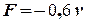, а початкові умови 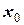= 0,2 м, 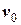= 2 м/с.

При даному закріпленні пружин сумарне зміщення вантажу (розтягнення двох пружин) є сумою їх розтягнень (окремих зміщень від початкового положення) тому

,

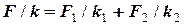і, оскільки

,

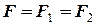ефективна жорсткість системи буде 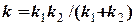= 60 Н/м.

Під дією сили тяжіння пружини будуть деформуватися, а величина статичної деформації може бути знайдена з умови

,

звідки

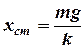= 0,1 (м).

Відносно цього положення і будуть здійснюватись коливання. В нашому випадку:

= 10 рад/с.

Тепер знайдемо значення величини :

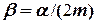= 0,5 с^-1.

Оскільки виконується умова < , то

,

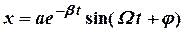і:

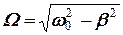= 9,99 (рад/с),

= 0,629 (с),

і ми маємо рівняння згасаючих коливань у вигляді:

.

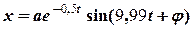Знайдемо величини 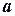та 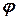з початкових умов. Спочатку знайдемо вираз для швидкості (взявши похідну від зміщення)

,

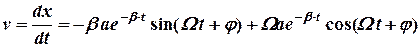після чого скористуємось початковими умовами і отримаємо:

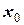= 0,2 = ,

= .

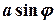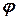Розв’язав останню систему рівнянь відносно і , отримаємо:

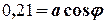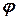( = 0,76 рад) та 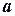= 0,3 м.

Таким чином, остаточно рівняння коливань має вид

(м).

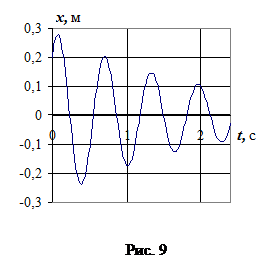
Графік цих коливань приведено на рис. 9.

Date: 2015-08-15; view: 480; Нарушение авторских прав