Для тех предикатов из 1), которые не являются ни тождественно истинными, ни тождестывенно ложными, указать область истинности и область ложности

a) Q ₁ = {2,3,…,N}

16. Доказать следующую равносильность: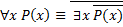

Доказательство:

Так как 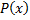– предикатная переменная, подставим вместо нее конкретный предикат 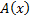и докажем, что:

По определению:

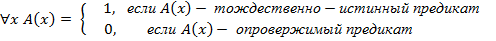
1) Пусть 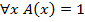, тогда предикат A (x) – тождественно-истинный, отсюда 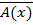– тождественно-ложный предикат, отсюда по определению связывания квантором существования по переменной x предиката B (x) получаем выказывание

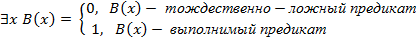
Отсюда следует, что высказывание 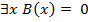, значит отрицание этого высказывания является истинным:

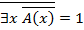
2) Пусть (*)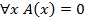

По определению:

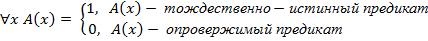
Из (*) следует, что 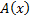– опровержимый предикат, тогда его отрицание 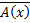- выполнимый предикат.

Тогда высказывание (**)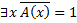

А отрицание высказывания (**) равно нулю:

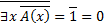
Доказать следующую равносильность:

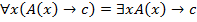
Доказательство:

По определению

(*)

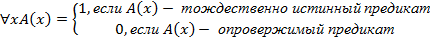1)Предположим, что

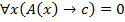
Тогда по определению (*),

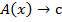– опровержимый, т.е.

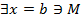-предмет, при котором 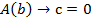. Получаем

,

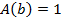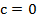
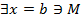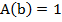Т.к. , что , то 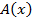- доказуемый предикат, т.е.

Тогда 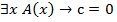при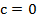

Следовательно

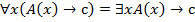
При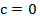

2) Предположим, что

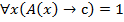
Тогда по определению (*),

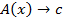– тождественно истинный, т.е.

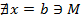-предмет, при котором 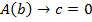. Получаем

Если 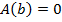, то значение c не важно

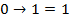
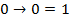
Если c=1, то значение 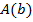не важно

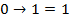
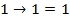
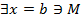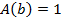Т.к. , что , то 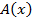- доказуемый предикат, т.е.

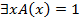
Тогда 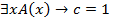при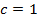

Следовательно

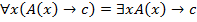
При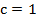

Доказать следующую равносильность:

1.

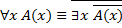
Законы де Моргана для кванторов

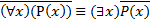
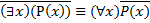
Доказательство.

Данная формула замкнута, т.е. не имеет свободных предметных переменных. Поэтому подставим в эту формулу вместо предикатной переменной 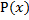любой конкретный одноместный предикат 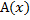, определенный на некотором множестве М=>получим высказывание

(*)

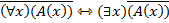-тавтология

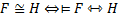
Для доказательства его истинности (*) нужно убедиться, что обе части эквивалентности одновременно истинны или одновременно ложны. В самом деле, высказывание 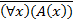истинно тогда и только тогда, когда высказывание 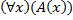ложно, что возможно, на основании определения, тогда и только тогда, когда предикат 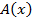-опровержим:

Далее, опровержимость предиката означает выполнимость предиката 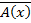, что равносильно истинности высказывания 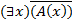(по определению)

Итак, высказывание 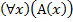истинно тогда и только тогда, когда высказывание 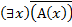истинно. Следовательно, высказывание (*) истинно, что и доказывает тождественную истинность первой формулы.

17. Найти отрицания следующих формул:

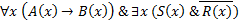
Решение:

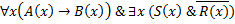
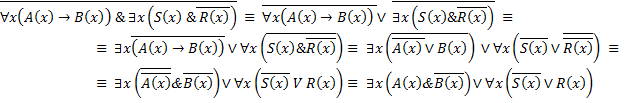
18. Даны два предиката Q (x, y) и R (y, z), определенные на множестве M 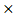M, где M = { a, b, c }. Записать без использования кванторных операций следующие формулы:

:

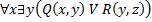Решение:

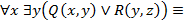
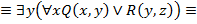
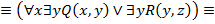
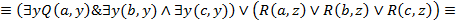
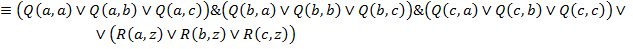
19. Привести к приведенной нормальной форме следующие формулы логики предикатов:

1)

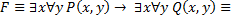
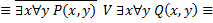
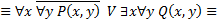
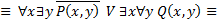
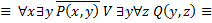
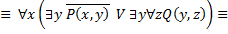
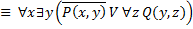
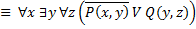
2)

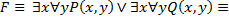
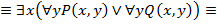
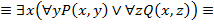
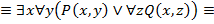
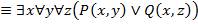
Литература

1. Игошин В.И. Математическая логика и теория алгоритмов. – Саратов: Издательство Саратовского университета, 1991.

2. Игошин В.И. Задачник-практикум по математической логике. – М.: Просвещение, 1986.

3. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. – 5-е изд. – М.: Физматлит, 2004, 256 с.

4. Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике. – М.: Физматлит, 2005, 416 с.

5. Яблонский С.В. Введение в дискретную математику. – М.: Физматлит, 2004, 384 с.

6. Лихтарников Л. М., Сукачева Т. Г. Математическая логика: курс лекций: задачник-практикум и решения. – СПб.: Лань, 2009, 288 с.

Содержание

§ 1. Основные понятия. 3

§ 2. Классификация предикатов. 3

§ 3. Множество истинности предиката. 4

§ 4. Равносильность предикатов. 5

§ 5. Логические операции над предикатами. 6

§ 6. Кванторные операции над предикатами. 10

§ 7. Численные кванторы.. 14

§ 8. Формулы логики предикатов. 16

§ 9. Классификация формул логики предикатов. 17

§ 10. Тавтологии (равносильности) логики предикатов. 19

§ 11. Равносильные преобразования формул. 21

§ 12. Общезначимость и выполнимость. 23

§ 13. Примеры и задачи. 27

§ 14. Решение примеров. 33

Учебное издание

Курочкина Ирина Алексеевна

Date: 2015-08-15; view: 1416; Нарушение авторских прав