Показатель преломления. Его физический смысл

Абсолютный показатель преломления показывает во сколько раз скорость света в вакууме с больше скорости света в среде v: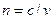

6. Почему, камень лежащий на дне водоема камень, кажется ближе?

Точечный источник света Р помещен в прозрачной однородной среде, огра­ниченной плоскостью. Световые лучи, исходящие из Р, испытывают преломление на этой плоскости. Найти для них каустическую поверхность.

Решение. Каустика преломленных лучей состоит из двух листов. Один из них есть геометрическое место фокальных точек меридиональных лучей, т. е. лучей, лежащих в плоскости падения главного луча элементарного астигма­тического пучка. Другой — геометри­ческое место фокальных точек эквато­риальных лучей, т. е. лучей, лежащих в перпендикулярной плоскости, про­ходящей через главный луч элемен­тарного пучка.

Пусть n — показатель преломления среды, в которой помещен источник Р.
Показатель преломления пространства, с которым граничит эта среда, примем за единицу. Введем прямоугольную систему координат с началом О, расположенным на границе среды. За ось Z примем нормаль к поверхности среды, направив эту ось в сторону точки Р (рис. 3.10). Ввиду осевой симметрии достаточно найти сечение каустической поверхности плоскостью, проходящей через ось Z. Прямую, вдоль которой эта плоскость пересекает границу среды, примем за ось X.

Найдем сначала каустику для меридиональных преломленных лучей, Уравнение преломленного луча АВ будет

z = -ctg φ^.(X—h^.tgψ)

где h— расстояние от точки Р до границы среды, ψ — угол падения из среды на эту границу, φ — угол преломления. Для бесконечно близкого луча РА'В' углы φ и ψ получат приращения dφ и dψ, Приращение координаты z при одном и том же значении абсциссы х при этом будет равно

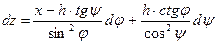
или с использованием закона преломления sin φ = n sin φ;

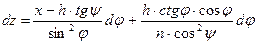
Координаты х_т и z_т точки Р_т,в которой пересекаются продолжения бесконечно близких меридиональных лучей АВ и А'В', найдутся отсюда, если приращение dz приравнять нулю. Это дает

,

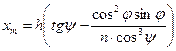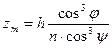
Это и есть уравнение каустики для меридиональных лучей. Используя его, нетрудно вывести формулу

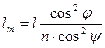(3.14)

где l — расстояние от предмета Р до точки выхода А преломленного луча, а l_т — расстояние меридионального изображения Р_т до той же точки.

Еще проще находится каустика для экваториальных лучей. Пусть РАB — один из лучей, исходящих из точки Р (рис. 54). Если этот луч вращать вокруг перпендикуляра ОР к преломляющей поверхности, то получится конус падающих и соответствующий ему конус преломленных лучей. Вершиной второго конуса будет точка Р_э, в которой продолжение преломленного луча АВ пересекает перпендикуляр РО. Бесконечно малые пучки падающих и преломленных лучей, лежащих на поверхностях указанных конусов, для которых луч РАВ является главным, будут, очевидно, расположены в плоскостях, перпендикулярных к плоскости падения луча РАВ. Значит, лучи этих пучков будут экваториальными, а точка Р_э — изображением в этих лучах. Таким образом, все фокальные точки экваториальных лучей расположатся на перпендикуляре РО, т. е. каус­тика таких лучей выродится в отрезок этого перпендикуляра. Расстояние l_э точки Р_э от точки выхода преломленного луча АВ будет Р_эА = l sin ψ/sin φ, т. е

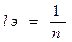(3.15)

Результаты вычислений представлены на рис.3.11 для п = 1,5 (стекло), Каустика экваториальных лучей представляется вертикальным отрезком ОР', длина которого равна h/п, Сечение каустики меридиональных лучей плоскостью рисунка есть кривая ВР'А, для которой Р' является точкой возврата. Продолже­ния преломленных лучей, изображенные на рисунке пунктирными прямыми, касаются кривой ВР'А.

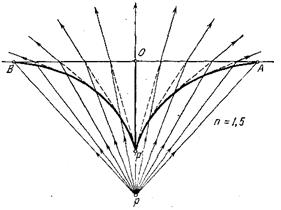
Рис. 3.11

1. Основные законы геометрической оптики.

Формулировка принципа. Ферма предположил, что распростра­нение света из одной точки в другую происходит по такому пути, прохождение которого требует меньше времени, чем любые другие пути между теми же точками. В этом заключается существо принципа Ферма, называемого также принципом наименьшего времени.

Согласно принципу наименьшего времени Ферма, вариация интеграла, которым определяется время распространения света, должна обращаться в нуль

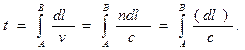(3.16)

Это и есть математическое выражение принципа Ферма.

Выражение (3.16) в действительности является более общим, чем принцип Ферма, сформулированный в своем первоначальном виде. Дело в том, что условие 8t = 0 не является условием только минимума; это есть условие экстремума — минимума, максимума или стационарности. Следовательно, свет при распространении между двумя точками может «выбирать» не только путь, требующий минимального времени прохождения, но также путь, требующий максимального времени, либо пути, требующие одинакового вре­мени. Все эти три случая станут более ясными на следующих кон­кретных примерах.

Закон прямолинейного распространения света в однородной среде как следствие принципа Ферма. Ввиду того что минимальное расстояние между двумя точками есть прямая линия, соединяющая эти точки, прямолинейное распространение света в однородной среде является прямым следствием принципа Ферма.

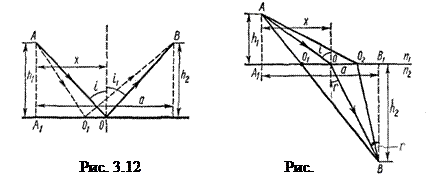
Вывод закона отражения. Из точки А направим луч света на зеркальную поверхность (рис. 3.12). Отраженный от зеркала луч достигает точки В, Исходя из принципа Ферма, определим путь, тре­бующий минимального времени распространения из точки А в точку В. Опустим нормали из точек А и В к зеркальной поверхности. Вве­дем обозначения: А₁О = х, А₁В₁ = а = const, АА₁ = h₁, ВВ₁ = h₂. Время, требуемое для распространения света из точки А в точку В с условием отражения от зеркальной поверхности, равно

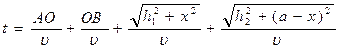(3.17)

где υ — скорость распространения света. Как видим, время рас­пространения света зависит от положения точки О, т. е. от пере­менной х. Тогда согласно принципу Ферма имеем

(3.18)

Отсюда sin i + sin i₁ = 0 и i = - i₁ , Знак минус показывает, что углы iи i₁ расположены по разным сторонам нормали к поверхности.

Следовательно, как вытекает из принципа Ферма, минимальным является путь, при котором имеет место известный нам закон отражения.

Вывод закона преломления. Пусть имеем две граничащие проз­рачные среды с показателями преломления п₁ и п₂ (рис. 3.13). Луч, вышедший из точки А первой среды, после преломления на границе раздела будет следовать по некоторой прямой OS. Докажем, исходя из принципа Ферма, что луч света из точки А в точку В распростра­нится в соответствии с законом преломления sin i/ sin r =n₂/n₁

Как и в предыдущем случае, обозначим: А₁О = х, А₁В₁ = а = const, АА₁ = h₁, ВВ₁ = h ₂. Тогда время, требуемое для распро­странения света из точки А в точку В, равно

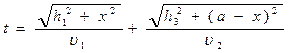(3.19)

где υ ₁ и υ ₂ — скорости распространения света соответственно в пер­вой и во второй средах. Время распространения света зависит от положения точки 0, Согласно принципу Ферма, луч света из всевозможных путей (АОВ, АО₁В, АО₂В и т. д.) «выберет» тот, который требует минимального времени распространения, т.е. будет реаль­ным тот путь, для которого имеет место dt = 0. Следовательно,

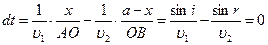(3.20)

Отсюда

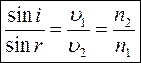(3.21)

Поскольку любой путь от точки А до точки В, лежащий вне плоско­сти, проведенной через точки А и В нормально к границе раздела *, проходится светом за большее время, чем путь АОВ, лежащий в плоскости падения, то из принципа Ферма следует: путь, требую­щий минимального времени, лежит в плоскости падения, т. е. па­дающий и преломленные лучи лежат на одной плоскости — плоско­сти падения. Аналогичное положение имеет место и при отражении света от границы раздела двух сред.

ЛАБОРАТОРНАЯ РАБОТА № 4