Числовая апертура объектива и разрешающая способность микроскопа

Разрешающая сила. Большая дисперсия оптических приборов является необходимым, но не достаточным условием для раздельного наблюдения двух близлежащих линий. Нами уже было отмечено, что контур максимума данной линии зависит от характеристик прибора. В зависимости от крутизны кривой интенсивности соседние максимумы длин волн λ₁ и λ₂могут наблюдаться как два самостоя­тельных (рис. 3.7, а) или как одни максимум (рис. 3.7, б). Как мы видим, величина дисперсии для двух близлежащих линий λ₁ и λ₂, имеющих контур, изображенный на рис. 3.7, б не позволит различить их в противоположность тем же максимумам λ₁и λ₂другого контура, изображенного на рис. 3.8. Важным фактором для различия этих линии является достаточная резкость спада к нулю кривых интенсивностей для λ₁ и λ₂(рис. 3.8). Чтобы характеризовать способность прибора при данной дисперсии различать две близлежащие линии, вводится понятие разрешающей силы. Для количественной характеристики этого понятия нужно ввести критерий разрешения.

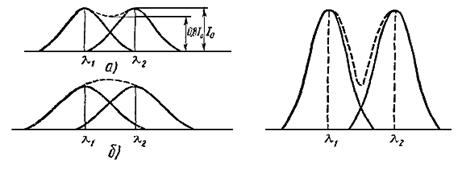Согласно Рэлею, две близлежащие спектральные линии с равными интенсивностями и одинаковыми симметричными контурами разрешимы, если максимум одной длины волны λ₁ совпадает с минимумом другой λ₂, и наоборот (см. рис. 3.7, а). При удовлетворении этого условия интенсивность «провала» между максимумами составляет 80% интенсивности каждой линии, что является достаточным для раздельного наблюдения линий λ₁и λ₂. Нарушение критерия Рэлея (см. рис. 3.7, б) приводит к наблюдению одной линии вместо двух.

Если разность длин волн | λ₂— λ₁|между двумя соседними максимумами, для которых выполняется критерий Рэлея, обозначить через δλ, а среднюю длину волны, соответствующую центру провала между максимумами, — через λ, то в качестве количественной характеристики разрешающей силы (А)можно взять отношение λ/δλ, т. е.

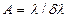(3.8)

Целесообразность введения такой количественной характеристики для разрушающей силы подтверждается тем, что она определяет уширение линии падающего излучения, связанного самим спектральным прибором.

Несмотря на условность критерия Рэлея, он позволяет сравнивать разрешающие силы разных приборов. Определим разрешающую силу разных спектральных приборов.

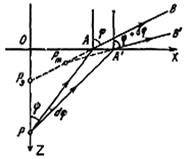
Разрешающая сила объектива. Положим, что параллельный пучок света падает на объектив диаметром D. Вследствие ограни­чения фронта волны оправой объектива возникает дифракционная картина в виде концентрических колец. Угловой (вершина угла совпадает с центром объектива) радиус первого темного кольца равен, как известно,

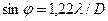
Если фокусное расстояние линзы обозначить через f, то радиус пер­вого темного кольца будет r= f tgφ. При малых значениях угла tg φ ≈ sin φ и

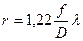(3.9)

Следовательно, каждая точка, лежащая на бесконечно большом расстоянии от объектива, даст в фокальной плоскости свою дифрак­ционную картину, радиусы первых темных колец которой опреде­ляются по формуле (3.9). Рассмотрим в объектив две близлежа­щие бесконечно удаленные точки. В зависимости от расстояния между ними происходит в той или иной степени взаимное перекрывание дифракционных картин. Вследствие некогерентности лучей, идущих от каждой точки, происходит простое сложение максимумов и минимумов. В зависимости от степени перекры­вания дифракционных картин эти точки либо сливаются в одну, либо наблюдаются самостоятельно. Для раздельного наблюдения должен выполняться критерий Рэлея. Если угловое расстояние двух точек обозначить через ψ, то, по условию Рэлея, φ = ψ, т. е.

sin φ = sin ψ = 1,22λ/D

Поскольку точки расположены близко, то sinψ ≈ φ и ψ = 1,22 λ /D. В качестве разрешающей силы объектива принимается обратное значение ψ:

A= 1/φ= D/1,22λ (3.10)

Выражение (3.10) показывает, что разрешающая сила объектива прямо пропорциональна его диаметру и зависит от длины световой волны.

Разрешающая сила микроскопа. Явление дифракции на апертуре объектива ограничивает возможности микроскопа. Как и в других оптических приборах, для количественной характеристики способ­ности микроскопа вводится понятие его разрешающей силы.

Под разрешающей силой микроскопа понимается то минимальное расстояние (линейное или угловое) между близлежащими точками, при котором их еще можно наблюдать раздельно. Вследствие того что объект располагается на небольшом расстоянии от объектива (обычно чуть дальше фокуса объектива), в данном случае не будет наблюдаться точная картина фраунгоферовой дифракции. Однако, так как плоскость изображения ПП объектива находится на рас­стоянии, существенно превышающем диаметр объектива, проходя­щие лучи можно считать почти параллельными. Далее, при рас­смотрении дифракции этих лучей на апертурной диафрагме * MN объектива (рис. 3.9) можно будет использовать выводы фраунгоферовой дифракции на круглом отверстии.

Необходимо уточнить еще одну деталь, связанную с лучами, идущими от наблюдаемого объекта. Здесь возможны два случая: а) объект является самосветящимся, б) объект освещается. В первом случае очевидно, что лучи, идущие от разных точек объекта, не будут когерентными и возникает простое наложение дифракционных картин от разных точек источника.

Во втором случае, если освеще­ние объекта производится точечным источником, лучи, рассеянные отдельными точками объекта, являются когерентными (так как они исходят из одного и того же точечного источника). Рассмотрим эти случаи:

Объект является самосветящимся (некогерентное излучение).

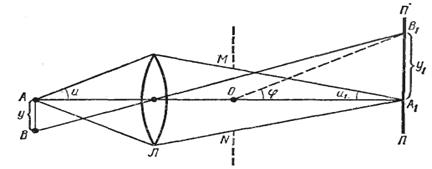
Рассмотрим две близлежащие точки объекта А и В, расположенные друг от друга на расстоянии у (рис. 3.9). Точки А ₁ и В ₁, располо­женные друг от друга на расстоянии y₁, являются изображениями точек А и В. Вследствие фраунгоферовой дифракции лучей на апертурной диафрагме MN, близко расположенной (иногда совпадающей) к оправе объектива (масштаб на рисунке искажен), точки А₁ и В₁ окружены соответствующими дифракционными кольцами. Согласно условию Рэлея, расстояние у₁ должно равняться радиусу первого темного кольца, окружающего А₁ (или В₁). Поскольку угловой ра­диус φ первого темного кольца определяется из условия MN sin φ = 1,22 λ, то линейный радиус первого темного кольца при малом угле φ будет

r₁=y₁=φOA₁=1,22λOA₁/MN=0,61λ/u₁

Отсюда

y₁u₁=0,61λ (3.11)

При получении (3.11) было использовано соотношение MN/OA₁ = 2u₁ (рис.3.9), справедливое для малого u₁.

Используя условие синусов, выполняющееся при правильном отображении объекта в микроскопе: y^.n^.sin u = y₁n₁sin u₁

имеем

y= y₁u₁/sin u=0,61λ/n^.sin u (3.12)

Следовательно, при некогерентном освещении самосветящегося объекта разрешающая сила микроскопа тем больше, чем больше числовая апертура и чем меньше длина волны света.

В случае если объект облучается со стороны, разрешающая сила микроскопа оказывается не более, чем в случае самосветящегося объекта.

Date: 2015-08-07; view: 1482; Нарушение авторских прав