Отражение и преломление света на границе двух однородных прозрачных диэлектриков

Граничные условия. Поставим перед собой задачу определения интенсивности отраженных и преломленных световых волн, а также их фаз и частот, опираясь на теорию поля Максвелла. Пусть пло­ская монохроматическая световая волна падает на плоскую, беско­нечно простирающуюся границу раздела двух однородных изотроп­ных прозрачных диэлектриков:

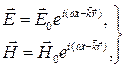(4.1)

По Максвеллу, свойства среды, в которой распространяются элек­тромагнитные волны, определяются ее макроскопическими харак­теристиками е и ц. Так как для всех прозрачных в видимой области тел 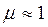, то имеем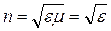

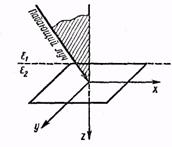
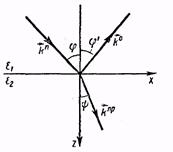
Направим ось OZ. перпендикулярно плоскости раздела по направлению ко второй среде. Ось OY проведем перпендикулярно падающему лучу и в направлении к наблюдателю (рис. 3.1) вдоль

границы раздела двух сред с диэлектри­ческими проницаемостями е_г и е_а. Сог­ласно граничным условиям, танген­циальные компоненты электрического и магнитного векторов остаются посто­янными во всех точках границы раздела для любого момента времени, т. е.

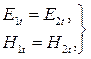
Из условия (3.2) вытекает наличие поля во второй среде, если на плоскость раз­дела из первой среды падает электромаг­нитная волна. Удовлетворить двум условиям, предполагая нали­чие только одной плоской волны, невозможно, так как равенства

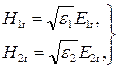(4.2)

РИС(4.1)

одновременно можно удовлетворить только при е^ = e%, что тривиально. Поэтому для решения задачи нужно предположить существование кроме падающей плоской волны еще, по крайней мере, двух плоских волн — отраженной и преломленной. Учиты­вая это, для электрических векторов соответствующих волн имеем:

падающая волна

отраженная волна

преломленная волна

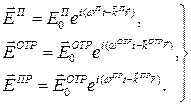(4.3)

Учитывая (3.4) в (3.2), получим

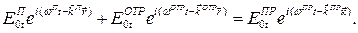(4.4)

Легко доказать, что условие (3.5) удовлетворяется при любом t и в любых точках плоскости раздела, если

(4.5)

Для доказательства (3.6) граничное условие (3.5) перепишем в сле­дующем виде:

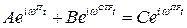(4.6)

где А, Б и С— величины, не зависящие от L Продифференцируем (3.5а) по времени:

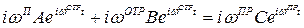(4.7)

Отсюда 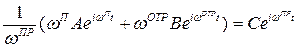(4.8) Сравнивая (3.5а) и (3.56), получим

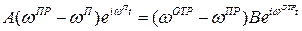(4.9)

Это равенство удовлетворится при любом t, если φ^п = φ^отр. Ана­логичным образом, определяя из уравнений (3.5а) и (3.5в) выраже­ния для Be^iωотрt и приравнивая их, получим φ^п = φ^пр, что и тре­бовалось доказать. Доказательство равенства компонентов волно­вых чисел принципиально ничем не отли­чается от вышеприведенного (вместо диф­ференцирования по времени проведем дифференцирование по координатам х и у).

Вывод законов отражения и прелом­ления. РИС(4.2) Если волновой вектор падающей волны лежит в плоскости xz, то 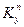= О и, следовательно, 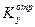= 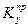, т. е. вол­новые векторы всех трех волн лежат в одной плоскости, которая, как при­нято, называется плоскостью падения (на рис. 3.1 эта плоскость заштрихована).

Если ввести углы падения ер, отражения φ' и преломления φ, то, как следует из рис. 3.2,

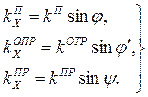(4.10)

Если принять во внимание, что 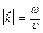то имеем:

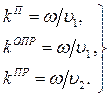(4.11)

где V₁ и У₂ — скорости распространения света соответственно в пер­вой и во второй средах. Из (3.6) — (3.8) имеем:

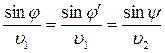(4.12)

Отсюда 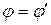и 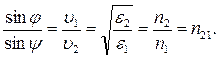(4.13)

3. Как известно, (3.9) и (3.10) есть законы отражения и преломле­ния света. Следовательно, предположение трех плоских монохро­матических волн, а также учет граничного условия дают воз­можность вывести известные из опытных данных законы отраже­ния и преломления, прийти к выводу о равенстве фаз и частот всех трех волн на границе раздела *.

4.

Date: 2015-08-07; view: 1080; Нарушение авторских прав