Таможенных систем

Одним из центральных моментов всего процесса принятия сис­темных решений в таможенном деле является формальная постановка за­дачи принятия решения.

Формализуем описание такой задачи в следующем виде.

1. Принятие решения представляет собой выбор одного из некоторого множества вариантов решений: Ei 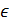E. Рассмотрим наиболее часто встре­чающийся на практике случай, когда имеется лишь конечное число вари­антов El, E2,..., Ei,..., Em. При необходимости предлагаемые формализ­мы без труда переносятся на этот общий случай.

2. Каждый вариант Е1 однозначно определяется некоторым результа­том ei. Эти результаты должны допускать количественную оценку, поэто­му для простоты будем отождествлять эти оценки с соответствующими результатами, обозначая их одним и тем же символом - ei.

Е = {<Ei (таможенная система) → ei (результат деятельности) → ei (оценка результата)>}.

Случай 1. Каждому варианту решения соответствует единственное со­стояние таможенной системы - случай детерминированных решений.

3. Пусть необходимо найти вариант с наибольшим значением резуль­тата, т. е. целью нашего выбора является max ei. При этом считаем, что оценки ei характеризуют такие величины, как, например, оперативность, стоимость или надежность. Противоположную ситуацию с оценкой затрат или потерь можно исследовать путем их минимизации.

Выбор оптимального варианта производится с помощью критерия

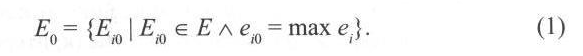
Это правило выбора читается следующим образом: множество Е₀ оп­тимальных вариантов состоит из тех вариантов E_io, которые принадлежат множеству Е всех вариантов и оценка которых максимальна среди всех оценок е_i. Логический знак ^ читается как «и».

Случай 2. Каждому допустимому варианту решения Е_i вследствие раз­личных внешних условий могут соответствовать различные состояния Е_j и результаты е_ij решений.

Постановка прикладной задачи. Пусть требуется оценить и при необ­ходимости определить эффективные решения по структуре и содержанию технологии таможенного оформления и контроля (ТО и ТК) в условиях автоматизации.

Варианты решений таковы:

Е₁ - выбор структуры из соображений максимальной автоматизации процесса ТО и ТК;

Е_m - выбор структуры в предположении минимальной автоматизации процесса ТО и ТК;

Е_i - промежуточные решения.

Условия, требующие рассмотрения, таковы: F₁ - условия, обеспечива­ющие максимальную автоматизацию; F_n - условия, обеспечивающие ми­нимальную автоматизацию; F_j - промежуточные условия.

Под результатом решения е_ij здесь можно понимать оценку, соответ­ствующую варианту Е_i и условиям F_j и характеризующую оперативность, стоимость или надежность ТО и ТК. Для общности будем называть такой результат полезностью решения.

Отображение решений. Семейство решений описывается некоторой матрицей решений 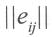(табл. 8).

Формирование целевой функции. Чтобы прийти к однозначному вари­анту решения, введем так называемые целевые (критериальные) функции, которые каждому варианту Е_i приписывают некоторый результат е_ir, ха­рактеризующий все последствия этого решения в целом. В этом случае матрица решений ||е_ij|| сводится к одному столбцу _ |e_ir|:

матрица решений ||е_ij|| → столбец решений |е_ir|, i = 1, 2,... m.

Процедуру выбора можно теперь представить по аналогии с примене­нием критерия (1).

Какой смысл вложить в результат е_ir?

Если, например, последствия каждого из альтернативных решений ха­рактеризовать комбинацией из его наибольшего и наименьшего результа­тов, то можно принять:

Для такого случая наиболее характерными являются целевые функ­ции.

1. Функция, определяющая компромисс между оптимистическим и пессимистическим подходами:

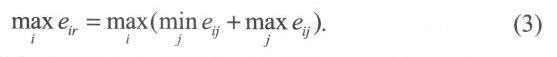
2. Функция, определяющая оптимистическую позицию в процессе выбора:

В данном случае аналитик делает ставку на полную автоматизацию и, исходя из этого, выбирает структуру технологии ТО и ТК.

3. Функция, определяющая позицию нейтралитета:

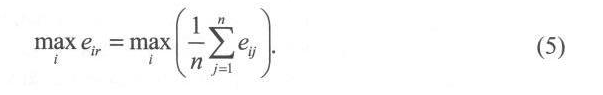
Аналитик исходит из того, что все встречающиеся отклонения резуль­тата решения от «среднего» случая допустимы, и выбирает размеры, оп­тимальные с этой точки зрения.

4. Функция, определяющая пессимистическую позицию:

Аналитик исходит из того, что надо ориентироваться на минимальное финансирование, а соответственно и на наименее благоприятный случай.

Определение поля выбора решений. Введем прямоугольную систему координат, откладывая по оси абсцисс значения результата решения е_i1, соответствующие внешнему состоянию F₁, а по оси ординат - значения е_i2 соответствующие состоянию F₂, i = 1,..., т. В этом случае каждый вариант решения Е_i, соответствует точке (е_i1, е_i2, I = 1,..., т на плос­кости.

Точку с координатами 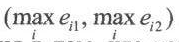назовем утопической точкой (УТ). Смысл этого названия в том, что координаты всех точек (е_i1, е_i2), i = 1,..., т, соответствующих вариантам решений E₁,..., Е_т, не могут быть больше, чем у точки УТ, и что УТ встречается среди s точек только в том редком идеальном случае, когда существует вариант решения, даю­щий максимальный результат для каждого из (двух) возможных внешних состояний.

Аналогичное значение имеет и так называемая антиутопическая точка (АУТ), имеющая координаты 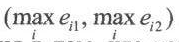: координаты всех точек (е_i1, е_i2), i = 1,..., т соответствующих вариантам решений E₁,..., Е_т, не могут быть меньше, чем у точки АУТ.

Отсюда следует, что все s точек (е_i1, е_i2), i = 1, ...,т лежат внутри прямоуголь­ника, стороны которого параллельны ко­ординатным осям, а противоположные вершины суть точки УТ и АУТ; назовем этот прямоугольник полем полезности решений (рис. 53).

Теперь, чтобы сравнить варианты ре­шений с точки зрения их качества, назо­вем вариант Е_i не худшим, чем вариант Е_j если для соответствующих точек (е_i1, е_i2) и (е_j1, e_j2) выполняются нера­венства e_i1 ≥ е_j1 и е_i2 ≥ е_j2, причем E_i считается лучшим, чем Е_j, если хотя бы одно из этих двух неравенств является строгим.

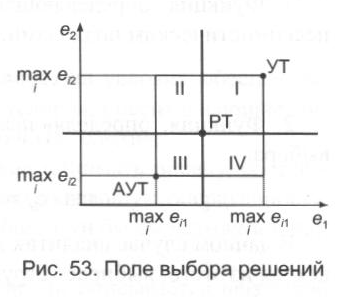
Очевидно, что при таком определении любые два варианта решений допускают сравнение в том смысле, что один из них оказывается лучше другого.

Выберем в поле полезности произвольную точку, которую будем назы­вать рассматриваемой (РТ). С помощью прямых, параллельных координат­ным осям, разобьем плоскость на четыре части и обозначим их I, II, III и IV.

Рассматривая положение точек поля полезности можно в общем слу­чае сказать следующее.

1. Все точки из конуса I лучше, чем рассматриваемая точка РТ. Поэто­му назовем квадрат I квадратом предпочтения.

2. Соответственно все точки из конуса III хуже точки РТ, и будем на­зывать область III антиквадратом. Таким образом, оценка качества точек из этих двух квадратов в сравнении с точкой РТ проста и однозначна.

3. Опенка точек в конусах II и IV является неопределенной, вследствие чего их называют областями неопределенности. Для этих точек оценка получается только с помощью специально формируемого критерия при­нятия решения. Например, критерий принятия решения можно предста­вить в виде:

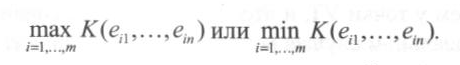
Таким образом, в неоднозначных условиях выбора и в условиях непол­ной информации:

• всякое решение сознательно или неосознанно принимается в соот­ветствии с какой-либо целевой функцией описанного выше типа;

• выбор целевых функций всегда должен осуществляться с учетом коли­чественных характеристик ситуации, в которой принимаются решения;

• эффективный поиск решений возможен только в рамках соответству­ющим образом сформированного поля выбора решений.

Date: 2015-08-06; view: 805; Нарушение авторских прав