Прогнозирование на основе рядов динамики и регрессионных моделей

Понятие ряда динамики. Виды рядов динамики

Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности чи­словых значений статистического показателя, характеризующих изменение общественных явлений во времени.

По времени, отраженному в динамических рядах, они разде­ляются на моментные и интервальные.

Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенные да­ты. Примером моментного ряда могут служить дан­ные о численности населения.

Интервальным рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени. Примером такого ряда могут служить данные о динамике добычи нефти в Российской Федерации.

По способу выражения уровней рядов динамики они могут быть рядами абсолютных, средних и относительных величин.

По расстоянию между уровнями ряды динамики подразде­ляются на ряды с равностоящими и неравностоящими уровнями по времени. Если в рядах динамики прерывающиеся или неравномерные интервалы времени, то такие ряды являются неравностоящими.

Показатели анализа ряда динамики. Прогнозирование на основе средних показателей ряда динамики

Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же ба­зисным уровнем. В качестве базисного выбирается либо началь­ный уровень в ряду динамики, либо уровень, с которого начи­нается какой-то новый этап развития явления.(базисные)

Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с преды­дущим. (цепные показатели)

Важнейшим статистическим показателем анализа динамики яв­ляется абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за оп­ределенный промежуток времени. Абсолютный прирост (цепной)=уровень сравниваемого периода – уровень предшествующего периода

Абсолютный прирост (базисный)= уровень сравниваемого периода – уровень базисного периода

Показатель интенсивности изменения уровня ряда, выра­женный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста.

Коэффициент роста: (цепной): Крц=у(i)-y(i-1)

Коэффициент роста: (базисный) Крб=у(i)-y(0)

Темп роста (цепной): Трц=у(i)/у(i-1)*100

Темп роста (базисный): Трб=у(i)/у(0)*100

Итак, Тр=Кр*100

Относительную оценку скорости измерения уровня ряда в еди­ницу времени дают показатели темпа прироста (сокращения).

Темп прироста (сокращения) показывает на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения.

Темп прироста (цепной): Тпрц=(сумма дельта У(ц))/У(i-1)*100

Темп прироста (базисный): Тпрб=(сумма дельта У(б))/У(0)*100

Средние показатели ряда динамики

Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической:

1) при равных интервалах применяется средняя арифметиче­ская простая:

Yср.пр.=(Y1+Y2+Y3…+Yn)/n

где у – абсолютные уровни ряда; п – число уровней ряда.

2) при неравных интервалах – средняя арифметическая взве­шенная:

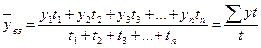,Yср.вз.=(Y1t1+Y2t2+…+YnTn)/(t1+t2+…+tn)

где 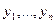– уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t; 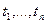– веса, длительность интервалов времени (дней, месяцев) между смежными датами.

Средний темп роста (снижения) – обобщенная характеристика индивидуальных темпов роста ряда динамики.

Кср.р.ц.=корень Nной степени из Крб

где п – число цепных коэффициентов роста; Крб – базисный ко­эффициент роста за весь период.

Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %.

Тср.пр=Тср.р-100

Кср.пр=Кср.р-1

где Тср.пр – средний темп прироста, Кср.пр – средний коэффициент прироста.

Прогнозирование на основе регрессионных моделей основывается на экстраполяции, т.е. продлении в будущее существующей тенденции.

Date: 2015-08-06; view: 1058; Нарушение авторских прав