Статистические распределения и их основные характеристики. Изучение корреляционной связи

Понятие ряда распределения. Атрибутивные и вариационные ряды распределения. Варианты, частоты и частности. Дискретные и непрерывные ряды. Построение дискретного и интервального вариационных рядов

Статистический ряд распределения представляет собой упо­рядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.

Ряды распределения, построенные по атрибутивным призна­кам, называются атрибутивными. (распределения населения по полу, занятости, национальности, профессии и т.д.)

Ряды распределения, построенные по количественному признаку, называются вариационными. (распределе­ние населения по возрасту, рабочих –по стажу работы, зара­ботной плате)

Вариационные ряды распределения состоят из двух элемен­тов: вариантов и частот.

Числовые значения количественного признака в вариацион­ном ряду распределения называются вариантами.

Частоты – это числа, показывающие, как часто встречаются те или иные варианты в ряду распределе­ния.

Вариационные ряды в зависимости от характера вариации под­разделяются на дискретные и интервальные. Дискретные вариаци­онные ряды основаны на дискретных признаках, имеющих только целые значения; интервальные – на непрерывных при­знаках.

Для построения дискретного ряда с небольшим числом вариантов выписываются все встречающиеся варианты значений признака, обозначаемые через x_i, а затем подсчитывается частота повторения каждого варианта f_i.

Для построения ряда распределения непрерывно изменяющихся признаков, либо дискретных, представленных в виде интервалов «от – до», необходимо установить оптимальное число групп, на которое следует разбить все единицы изучаемой со­вокупности.

Графическое изображение рядов распределения

Ряды распределения удобно изучать с помощью графического метода, позволяющего судить и о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон частот и гистограмма.

Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяются прямыми линиями, в результате этого получают ломаную линию, называемую полигоном частот.

Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков в случае равных интервалов должна быть пропорциональна частотам. В результате получим гистограмму – график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.

Понятие корреляционной связи. Поле корреляции.

Корреляционная связь – частный случай статистической связи, при котором разным значениям переменной соответствуют разные средние значения другой переменной. Корреляционная связь предполагает, что изучаемые переменные имеют количественное выражение.

В качестве примера на рис. 1 представлены данные, иллюстри­рующие прямую зависимость между х и у (рис. 1, а) и обратную зависимость (рис. 1, б). В случае «а» это прямая зависимость между, к примеру, среднедушевым доходом (х) и сбережением (у) в семье. В случае «б» речь идет об обратной зависимости. Такова, наш пример, зависимость между производительностью труда (х) и себе­стоимостью единицы продукции (у

а) б)

Рис. 1. Поле корреляции

Основные типы корреляции

В зависимости от направления действия функциональные и стохастические связи могут быть прямыми и обратными. При прямой связи направление измене­ния результативного признака совпадает с направлением изменения признака-фактора. В противном случае между рассматриваемыми величинами существуют обратные связи.

Прямолинейные и криволинейные связи. При прямолинейной связи с возрастанием значения факторного признака происходит непрерывное возрастание значений результативного признака.

При криволинейных связях с возрастанием значения факторного признака возрастание (или убывание) результативного признака происходит неравномерно или же направление его изменения меняется на обратное.

По количеству факторов, действующих на результативный признак, связи различаются однофакторные (один фактор) и многофакторные (два и более факторов).

Измерение корреляционной связи

Корреляционный анализ позволяет найти методы проверки того, что полученное числовое значение анализируемого измерителя связи действительно свиде­тельствует о наличии статистической связи. Наконец, он помогает определить структуру связей между исследуемыми k признаками 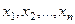, сопоставив каждой паре признаков ответ.

Date: 2015-08-06; view: 853; Нарушение авторских прав