Кристаллические фазовые пластинки

Рассмотрим нормальное падение (вдоль оси Oz) поляризованного света на поверхность пластинки, вырезанной параллельно оптической оси (оптической осью пусть служит ось Oy). Плоскостью главного сечения, следовательно, является плоскость yOz. Падающий на пластинку свет представим как совокупность двух волн, поляризованных вдоль оптической оси и перпендикулярно к ней (рис. 6.11).

Р и с. 6.11

Первая из них в пластинке будет необыкновенной волной (Е_е), вторая – обыкновенной (Е _об).

Направление распространения волн в пластинке можно найти по принципу Гюйгенса, в котором постулируется, что каждая точка анизотропной среды, до которой доходит световое возбуждение, может рассматриваться как центр двух вторичных волн: обыкновенной и необыкновенной. Т.к. скорость 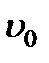обыкновенной волны одинакова во всех направлениях, то ей соответствует сферическая волновая поверхность. Скорость 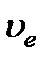необыкновенной волны зависит от направления ее распространения. Волновая поверхность необыкновенной волны имеет вид эллипсоида вращения, который в направлении оптической оси (оси вращения) должен касаться сферической волновой поверхности обыкновенной волны. В направлении, перпендикулярном оптической оси, обе поверхности расходятся сильнее всего. На рис. 6.12 представлено сечение волновых поверхностей плоскостью xOy.

Р и с. 6.12	Р и с. 6.13

Такой же вид будет иметь сечение и в плоскости yOz. Для определения положения волнового фронта распространяющейся волны в последующие моменты времени следует построить огибающую соответствующих волновых поверхностей. На рис. 6.13 А ₀ В ₀ представляет собой фронт обыкновенной волны, А_еВ_е – фронт необыкновенной волны. Прямые, проведенные из центра возбуждения вторичных волн в точки касания волновых поверхностей и фронтов, укажут направления распространения обыкновенного (о) и необыкновенного (е) лучей.

Как видно из рис. 6.13, при нормальном падении плоской волны на поверхность пластинки, вырезанной параллельно оптической оси, точки касания для обеих волн лежат на одной прямой, поэтому в пластинке обе волны распространяются в одном направлении, но с различными скоростями. В нашем примере необыкновенная волна движется быстрее обыкновенной (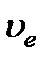 > 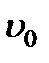). Такие кристаллы называются отрицательными.

Пусть плоскость поляризации падающего на пластинку поляризованного света составляет угол 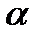с плоскостью главного сечения пластинки (плоскость yOz, рис. 6.11). Амплитуды А ₀ и А_е колебаний обыкновенной и необыкновенной волн будут равны, соответственно: ,

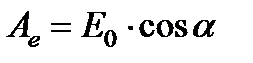, где Е ₀ – амплитуда колебаний в падающей волне.

Тогда компоненты вектора можно записать в виде

, .

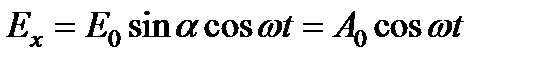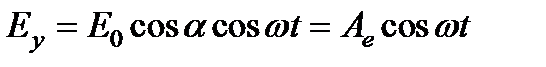Разность фаз между колебаниями в момент падения на пластинку равна нулю, если падающий свет имеет линейную поляризацию.

Поскольку скорости обеих волн различны, изменения фаз для них при прохождении через пластинку будут неодинаковы. Пренебрегая потерями на отражение, можно записать компоненты вектора для света, выходящего из пластинки, в ви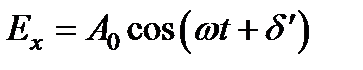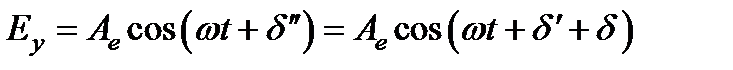де , , где , .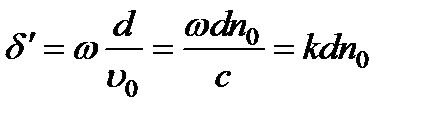

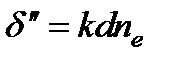Следовательно, вносимая пластинкой разность фаз 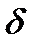и разность хода запишется следующим образом.

, .

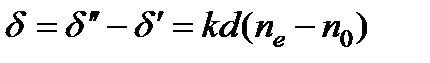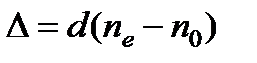После выхода из пластинки обыкновенный и необыкновенный лучи, складываясь, дают в общем случае свет эллиптической поляризации. Ориентация осей эллипса и соотношение между ними будут зависеть от поляризации падающего на пластинку света, толщины и ориентации пластинки.

Действительно, исследуем напряженность электрического поля суммарного колебания в плоскости, перпендикулярной направлению распространения волн, т.е. при фиксированном значении z. С течением времени конец вектора 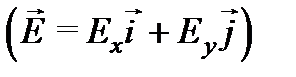описывает в плоскости xOy некоторую замкнутую кривую. Найдем уравнение этой кривой, исключив время t. Перепишем в виде:

.

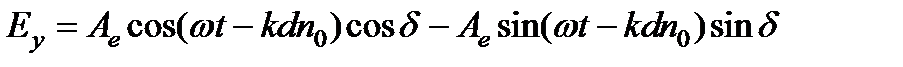Исключим из этого равенства 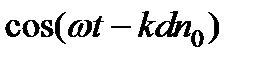и 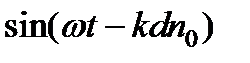с помощью формулы, тогда .

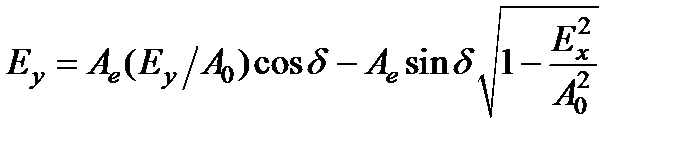Перенесем первое слагаемое правой части на левую сторону, возведем обе части в квадрат, раскроем квадрат и после перегруппировки членов приводим уравнение к виду

.

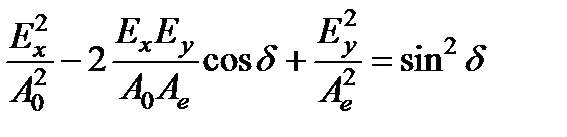Это есть уравнение эллипса, форма и ориентация которого относительно осей зависит от значени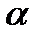й и 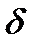(значение 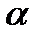определяет соотношение между А ₀ и А_е). Следовательно, при прохождении линейно поляризованного света через кристаллическую пластинку получаем световую волну, конец вектора которой описывает за период эллипс в плоскости xOy при фиксированном значении z. Такой свет называется эллиптически поляризованным. Рассмотрим некоторые частные случаи.

Толщина пластинки такова, что разность хода двух волн составляет четверть волны 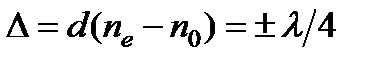. Такая пластинка называется пластинкой в четверть длины волны (пластинка ^” λ /4^”). Согласно, на выходе из пластинки разность фаз равна 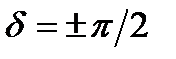(с точностью до 2 π), а выходящий из нее свет поляризован эллиптически. Уравнение принимает вид .

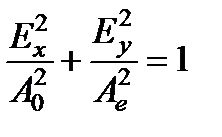Это выражение есть уравнение эллипса с центром в начале координат и осями, направленными вдоль главных направлений кристалла. (Главными направлениями являются направление оптической оси и направление, перпендикулярное ей).

Если пластинка расположена так, что 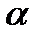= π /4, то амплитуды колебаний в обыкновенной и необыкновенной волнах одинаковы (A ₀ = A_е) и на выходе из пластинки свет поляризован по кругу.

В случае правой круговой поляризации sin δ >0, так что 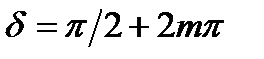, где (m = 0, ±1, ±2,...) и формулы и примут вид: , 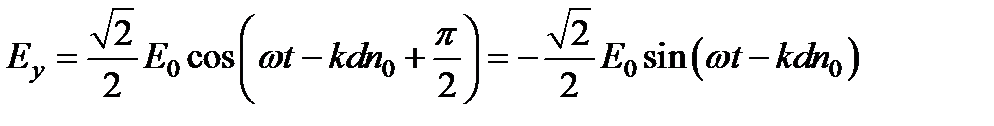. Для левой поляризации sin δ <0, так что 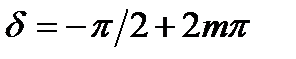, где (m = 0, ±1, ±2,...).

Соответственно , .

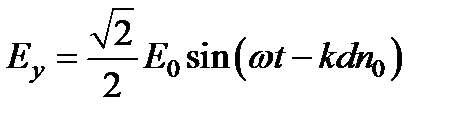С помощью пластинки ^” λ /4^” можно выполнить и обратную операцию: превратить эллиптически поляризованный свет в линейно поляризованный. Если оптическая ось пластинки совпадает с одной из осей эллипса поляризации, то в момент падения света на пластинку между компонентами уже имеется начальная разность фаз π /2. После пластинки разность фаз (с точностью до величины 2 π) становится равной 0 или π. Поэтому обыкновенные и необыкновенные волны, складываясь, дают линейно поляризованный свет. Пластинка ^” λ /4^” способна перевести в линейно поляризованный свет и свет круговой поляризации, при этом положение пластинки безразлично.

Для пластинки в целую длину волны λ разность хода равна .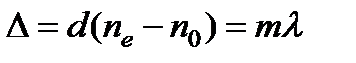

Выходящий из пластинки в этом случае свет остается поляризованным линейно, причем плоскость колебаний не изменяет своего направления при любой ориентации пластинки. Формула принимает вид .

Это есть уравнение прямой. Прямая лежит в (1–3) квадрантах (рис. 6.14).

Р и с. 6.14

Значит на выходе из пластинки ^” λ ^” имеется поляризованная волна с той же плоскостью колебаний вектора Е, что и на входе. В случае пластинки ^” λ /2^” разность хода и разность фаз запишутся соответственно:

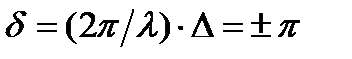, и уравнение эллипса вырождается в прямую.

.

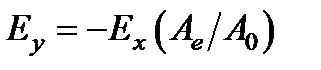Выходящий из пластинки свет при этом остается линейно поляризованным, но плоскость колебаний поворачивается против часовой стрелки на угол 2 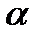относительно направления оптической оси (оси Oy). (см. рис. 6.14 – пунктирная линия).

Date: 2015-08-06; view: 558; Нарушение авторских прав