Преломление на границе анизотропной среды. Построения Гюйгенса

Полное количественное решение задачи о преломлении и отражении света на границе анизотропной среды может быть получено на основе электромагнитной теории. Как и в случае границы изотропных сред, электромагнитное поле должно удовлетворять тем же граничным условиям: тангенциальные составляющие векторов и 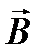по обе стороны границы должны совпадать в каждой ее точке в любой момент времени. Метод решения задачи остается прежним: в первой среде наряду с заданной падающей монохроматической плоской волной рассматривается еще одна – отраженная, а во второй среде – преломленная. Отличие состоит в том, что для волн в анизотропной среде нужно учитывать зависимость фазовой скорости от направлений волновой нормали и поляризации. Эта зависимость может быть найдена с помощью уравнений Максвелла и материальных уравнений примерно так, как это было сделано для лучевой скорости в одноосных кристаллах.

Электромагнитная теория позволяет найти как направления отраженной и преломленных волн, так и их амплитуды. Однако в общем случае окончательные формулы оказываются чрезвычайно громоздкими. Поэтому ограничимся лишь иллюстрацией применения электромагнитной теории на наиболее простом примере.

Пусть плоская волна падает из вакуума (или воздуха) на границу оптически одноосной анизотропной однородной среды, занимающей верхнее полупространство (рис. 6.8). Рассмотрим частный случай: оптическая ось параллельна границе ху и перпендикулярна плоскости падения xz (т.е. параллельна оси у). Падающую волну разложим на составляющие, поляризованные в плоскости падения и в перпендикулярном направлении. Граничные условия, как и для изотропной среды, выражаются уравнениями (5.36). Чтобы эти условия выполнялись сразу во всех точках границы, у всех трех экспонент зависимость от координат х и у должна быть одинакова. Отсюда, во-первых, следует, что у волновых векторов 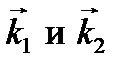отраженной и преломленной волн равны нулю y -составляющие, т.е. нормали к волновым поверхностям отраженной и преломленной волн лежат в плоскости падения. Во-вторых, из равенства x -составляющих векторов 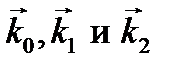следуют геометрические законы отражения и преломления, определяющие направления этих волн. Так как k _{0 x} =(ω / с)sin φ, k _{1 x} = (ω / с)sin φ ₁, то φ ₁= φ: угол отражения φ ₁ от анизотропной среды равен углу падения φ.

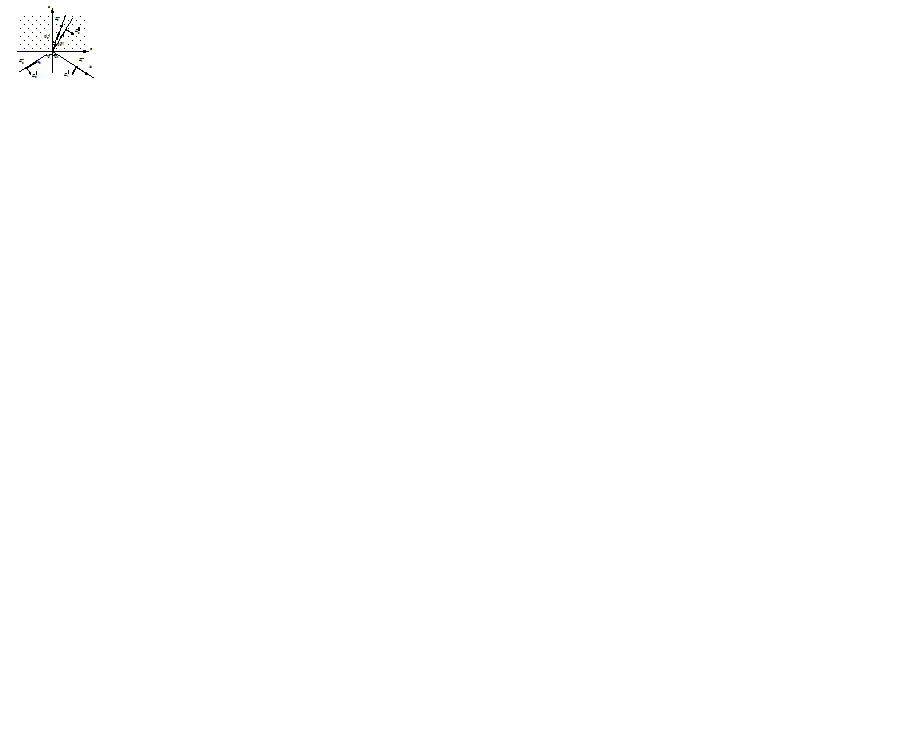
Р и с. 6.8

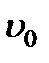Что касается угла преломления φ ₂ , то теперь он будет иметь разные значения для двух ортогональных поляризацией. В самом деле, при рассматриваемом направлении оптической оси (вдоль оси у) в волне, поляризованной в плоскости падения, вектор направлен перпендикулярно оптической оси. Скорость такой (обыкновенной) волны равна 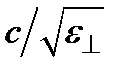=с/ п ₀, а модуль ее волнового вектора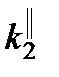 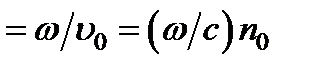. Из 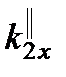= k _0x, учитывая, что 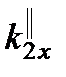= 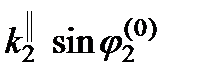, находим 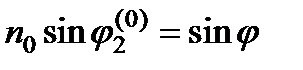. Если же волна линейно поляризована в направлении, перпендикулярном плоскости падения, то для рассматриваемого расположения вектор в ней направлен вдоль оптической оси. 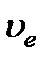Скорость этой (необыкновенной) волны равна 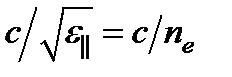, а модуль волнового вектора 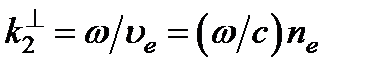. Поэтому для нее угол преломления 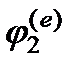определяется из условия 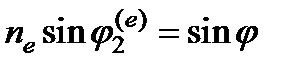. Так как здесь скорость необыкновенной волны одна и та же для любого ее направления в плоскости xz, то отношение синусов угла падения и угла преломления постоянно и равно n_е. Полученные выше выражения для 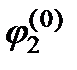и определяют направления волновых нормалей преломленных волн. Для сравнения с опытом важно знать ход лучей, представляющих пути распространения световой энергии. Однако при выбранном расположении преломленные волны идут перпендикулярно оптической оси, когда лучи и волновые нормали совпадают. Таким образом, в этом частном случае падающий из вакуума под углом 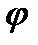луч создает два преломленных луча (обыкновенный и необыкновенный), углы преломления которых 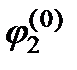и (рис. 6.8) даются соотношениями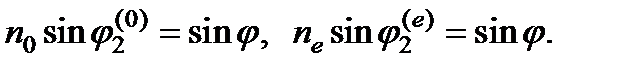

Граничные условия позволяют найти не только направления отраженной и преломленных волн, но и их амплитуды. Действуя так же, как и в § 5.4, мы в рассматриваемом случае придем к таким же формулам Френеля (5.65–5.68) с той лишь разницей, что для поляризации, перпендикулярной плоскости падения, выражения для амплитуд отраженной и преломленной волн содержат п_е в качестве показателя преломления второй среды и угол преломления из вместо :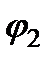

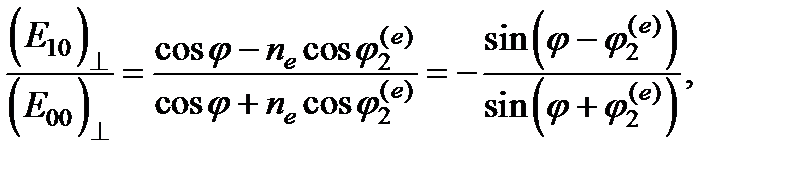
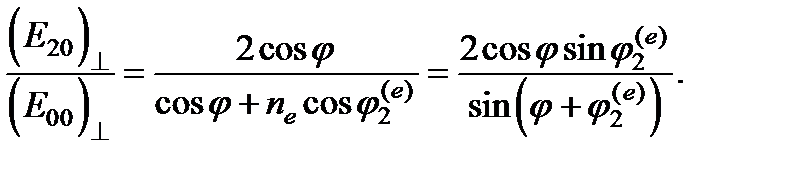Составляющая падающей волны, поляризованная в плоскости падения, преломляется на иной угол 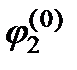, и для нее амплитуды отраженной и преломленной волн выражаются соответствующими формулами Френеля с заменой n ₂ на п ₀ и φ ₂ на :

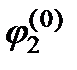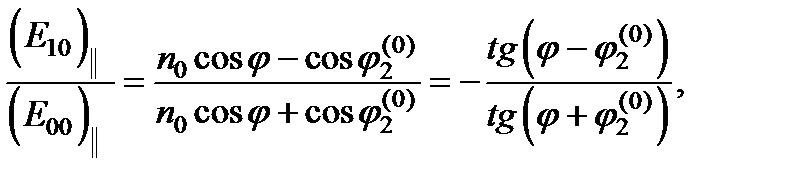
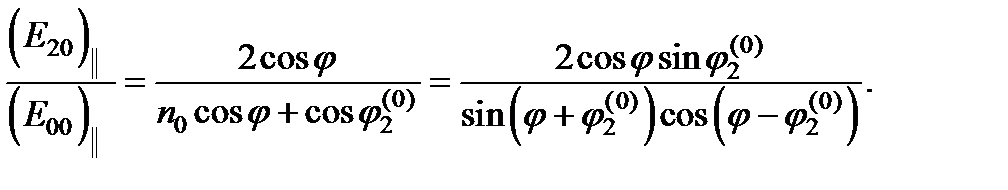
Мы видим, что в данном случае электромагнитная теория дает исчерпывающее описание отражения и преломления света на границе анизотропной среды. При ином расположении оптической оси относительно границы принципиальные затруднения не возникают, но вычисления оказываются громоздкими. В таких случаях возможно получить частичное решение задачи – определить направления преломленных волн в одноосном кристалле – с помощью изящного геометрического построения, впервые примененного Гюйгенсом для объяснения двойного лучепреломления в исландском шпате.

Р и с. 6.9

Напомним, как выполняется построение Гюйгенса в случае изотропной среды (рис. 6.9). Когда волновая поверхность падающей из вакуума плоской волны достигает точки 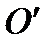на границе изотропной среды, она становится источником вторичной волны, распространяющейся во второй среде со скоростью 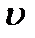=с/п. Вторичные волны от всех точек границы раздела (между точками 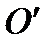и О) имеют общую огибающую ОВ, которая и представляет собой поверхность равных фаз преломленной волны. Учитывая, что вторичная волна проходит расстояние О'В за то же время, что падающая волна расстояние АО, из треугольников ОО'А и ОО'В получаем закон преломления: sin φ = n sin φ ₂.

При обобщении построений Гюйгенса на случай анизотропной одноосной среды для вторичных волн нужно использовать найденные раньше поверхности лучевых скоростей. Касательная к ним плоскость дает положение фронта (т.е. поверхности равных фаз) преломленной волны, а прямая, проведенная из центра вторичной волны в точку касания, – направление преломленного луча. Так как лучевая поверхность состоит из сферы и эллипсоида, то построение Гюйгенса дает два луча: обыкновенный, направление которого совпадает с нормалью к фронту, как и в изотропной среде, и необыкновенный, направление которого в общем случае отклоняется от нормали к фронту необыкновенной волны.

Для иллюстрации построений Гюйгенса рассмотрим несколько сравнительно простых частных случаев.

А. Оптическая ось параллельна границе. Плоскость падения перпендикулярна оптической оси (рис. 6.10, а). Сечения лучевых поверхностей обыкновенной и необыкновенной волн представляют собой окружности. Поэтому направления лучей и волновых нормалей совпадают как у обыкновенной, так и у необыкновенной волн. Вектор в обыкновенной волне ориентирован перпендикулярно оптической оси, в необыкновенной – параллельно оси. Точки и стрелки на рисунке показывают направление колебаний электрического вектора волны. При п ₀ >п_е (отрицательный кристалл) обыкновенный луч преломляется сильнее, чем необыкновенный: 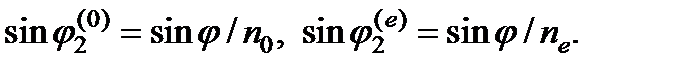Этот случай для положительного кристалла был рассмотрен выше на основе электромагнитной теории.

Б. Оптическая ось параллельна границе. Плоскость падения проходит через оптическую ось (рис. 6.10, б). Сечения лучевых поверхностей плоскостью падения – окружность и эллипс, соприкасающиеся вдоль оптической оси. Направление преломленного луча задается прямой, проведенной из центра лучевой поверхности в точку ее касания с огибающей (т.е. с фронтом волны). Оба преломленных луча лежат в плоскости падения. При п ₀ >п_е необыкновенный луч преломляется сильнее, чем обыкновенный, хотя направление волновой нормали для него (в данном случае не совпадающее с лучом) изменяется при преломлении меньше, чем для обыкновенного луча. Если свет падает по нормали (φ =0), то обе волны будут распространяться в прежнем направлении, но с разными скоростями.

В. Оптическая ось перпендикулярна границе (рис. 6.10, в). Оба преломленных луча лежат в плоскости падения. При п ₀ >п_е обыкновенный луч преломляется сильнее, чем необыкновенный. Если для обыкновенного луча 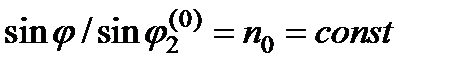, то для необыкновенного 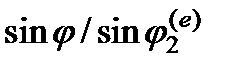зависит от угла падения. При нормальном падении обе волны распространяются в прежнем направлении (вдоль оси) с одинаковой скоростью, т. е. нет двойного лучепреломления. Состояние поляризации волны в кристалле будет таким же, как у падающей волны.

Р и с. 6.10

Г. Оптическая ось образует произвольный угол с преломляющей гранью кристалла. Свет падает по нормали (рис. 6.10, г). Волновые поверхности обыкновенной и необыкновенной волн (т.е. касательные к сферам и эллипсоидам) представляют собой плоскости, параллельные границе. Из расположения точек касания этих плоскостей с эллипсоидальными лучевыми поверхностями ясно, что необыкновенные лучи при нормальном падении отклоняются от первоначального направления. Этим объясняется двойное лучепреломление при нормальном падении света на естественную грань кристалла.

При наклонном падении света преломление становится еще сложнее. Если оптическая ось не лежит в плоскости падения, то по положению точек касания огибающей плоскости с эллипсоидами вторичных волн можно установить, что необыкновенный луч при преломлении выходит из плоскости падения.

Из рассмотренных примеров видно, что построение Гюйгенса дает наглядную картину двойного лучепреломления и позволяет сравнительно просто найти направление обыкновенной и необыкновенной преломленных волн. Однако оно оставляет открытым вопрос об их амплитудах, фазах и поляризации.

Date: 2015-08-06; view: 1808; Нарушение авторских прав