Плоские монохроматические волны в анизотропной среде. Одноосные кристаллы

Рассмотрим распространение света в прозрачной анизотропной среде на основе электромагнитной теории. Уравнения Максвелла для электромагнитного поля в веществе имеют универсальный характер и в полной мере применимы к анизотропным средам. Будем искать их решение в виде плоских монохроматических волн, где 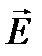, , 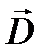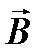зависят от координат и времени по закону 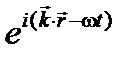. Введем единичный вектор волновой нормали 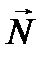, направленный вдоль волнового вектора 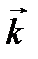(то есть перпендикулярно плоскостям равных фаз):

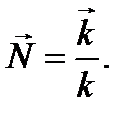Тогда из уравнений Максвелла получим: .

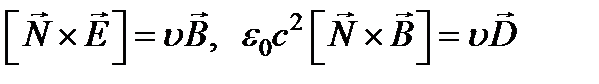Здесь 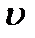– фазовая скорость волны, т.е. скорость, с которой поверхность равных фаз перемещается в направлении волновой нормали 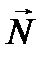. Прежде чем вводить материальное уравнение, связывающее векторы 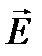и 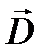в анизотропной среде, рассмотрим те свойства электромагнитных волн, которые следуют непосредственно из уравнений. Эти свойства отражают взаимное расположение векторов 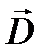, , 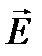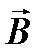и 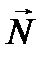. Из второй формулы видно, что вектор 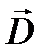перпендикулярен векторам 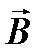и 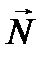, а из первой – что векторы 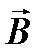и 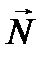взаимно перпендикулярны. Таким образом, в бегущей волне векторы 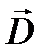, 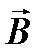и 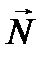образуют правую тройку ортогональных векторов (рис. 6.4). Что касается вектора 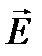, то в анизотропной среде его направление, вообще говоря, не совпадает с направлением 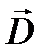. Из первого уравнения следует, что вектор 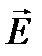ортогонален вектору 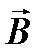, то есть лежит в плоскости, образуемой векторам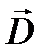и и 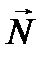. Это значит, что бегущие волны в анизотропной среде поперечны в отношении векторов 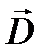и 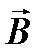, но в общем случае они не поперечны в отношении вектора 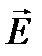(рис. 6.4). Направление переноса энергии в электромагнитной волне определяется вектором Пойнтинга 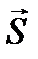. Для характеристики этого направления введем ориентированный вдоль единичный вектор : .

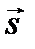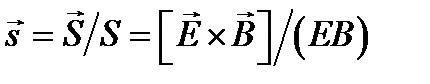Р и с. 6.4

Его называют лучевым вектором, так как направление переноса энергии – это и есть направление лучей. В изотропной среде лучи параллельны волновой нормали. Однако в анизотропной среде в общем случае это не так. Из рис. 6.4 видно, что вектор 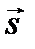, ортогональный векторам 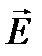и 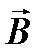, лежит в одной плоскости с 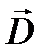, 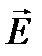и 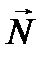и составляет с вектором 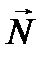такой же угол 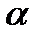, что и вектор 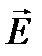с .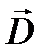

Плоскость равных фаз перемещается вдоль вектора 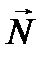со скоростью 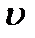. Скорость перемещения этой плоскости вдоль вектора луча называется лучевой скоростью и. Когда 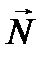и не совпадают, лучевая и фазовая скорости не равны и, как видно из рис. 6.4, связаны соотношением .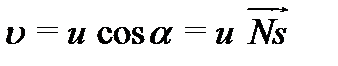

Особенности распространения лучей (т.е. переноса энергии) в анизотропной среде обусловлены как дисперсией волн (т.е. зависимостью фазовой скорости от частоты), так и отличием направлений волновых нормалей 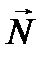и лучей . Дисперсия в равной мере присуща как изотропным, так и анизотропным средам. Чтобы выделить особенности, специфичные только для анизотропной среды, будем в дальнейшем пренебрегать дисперсией, т.е. полагать 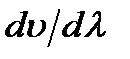=0. В такой недиспергирующей среде вектор лучевой скорости 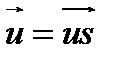характеризует направление и скорость переноса энергии световой волны. Поэтому задача определения лучевой скорости в зависимости от направления луча представляет наибольший интерес и на ее решении будет сосредоточено основное внимание.

Преобразуем уравнения так, чтобы вместо вектора волновой нормали 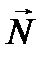в них фигурировал лучевой вектор 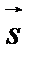, а вместо фазовой скорости 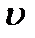– лучевая скорость и. Для этого умножим векторно левую и правую части каждого из них на 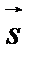. Двойные векторные произведения в левых частях преобразуются следующим образом: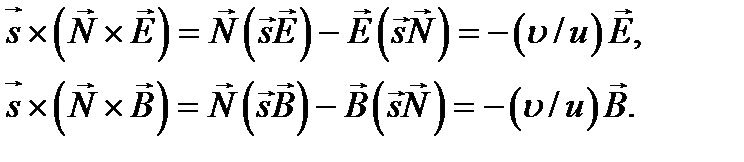

Здесь мы воспользовались тем, что вектор 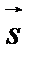в соответствии с ортогонален векторам и 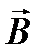, а произведение заменили на 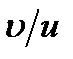с помощью формулы. В результате вместо получаем

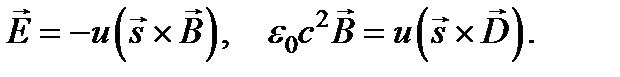
Теперь можно исключить из этих уравнений индукцию 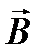магнитного поля: 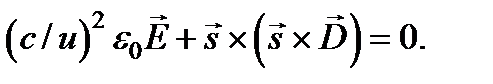Раскрывая двойное векторное произведение и учитывая, что 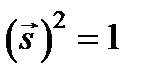, получаем уравнение, которому должны удовлетворять и в бегущей плоской волне: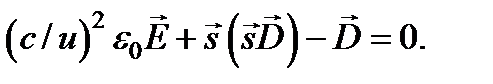

Cоотношения и получены на основе уравнений Максвелла без каких бы то ни было предположений о свойствах среды. Чтобы продвинуться дальше, необходимы материальные уравнения, связывающие и 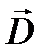в рассматриваемой среде. В анизотропной среде поляризованность , в общем случае не совпадает по направлению с создающим ее электрическим полем . Поэтому не совпадают и направления и 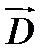, т.е. в материальном уравнении, связывающем и 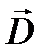в монохроматической волне, диэлектрическая проницаемость 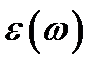представляет собой тензор второго ранга: .

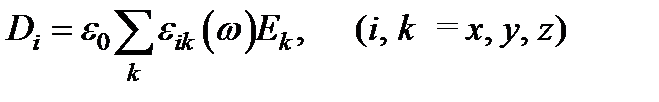Компоненты тензора диэлектрической проницаемости для той или иной модели среды могут быть рассчитаны на основе электронной теории дисперсии. В рамках феноменологической теории (которая положена в основу дальнейшего рассмотрения) их можно считать параметрами, определяемыми на опыте.

В различных системах координат х, у, z компоненты тензора 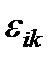имеют разные значения. Специальным выбором системы координат соотношение можно упростить, приведя тензор 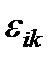к диагональному виду: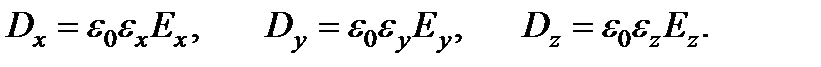

Если вектор направлен вдоль одной из этих осей, то вектор 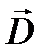совпадает с ним по направлению. Соответствующие оси координат х, у, z называются главными осями тензора, а величины 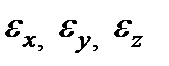– его главными значениями или главными диэлектрическими проницаемостями. Различие главных значений и отражает несовпадение направлений векторов и 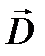(рис.6.5). Если два главных значения диэлектрического тензора 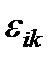совпадают 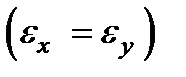, то среда оптически одноосная. Ее оптические свойства полностью определяются двумя параметрами 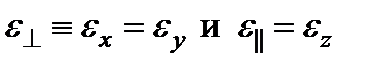, называемыми поперечной и продольной диэлектрическими проницаемостями. Когда вектор лежит в плоскости ху, т.е. перпендикулярен оси z (направление которой параллельно оптической оси), вектор совпадает с ним по направлению. Это значит, что в отношении оптических (и электрических) свойств одноосная среда обладает полной симметрией вращения относительно направления оптической оси, хотя в отношении других свойств (например, механических) симметрия может быть более низкой.

К оптически одноосным средам относятся все кристаллы тетрагональной, гексагональной и тригональной (ромбоэдрической) систем; оптическая ось совпадает здесь с осью симметрии соответственно четвертого, шестого или третьего порядка. Изотропное твердое тело (например, стекло), подверженное однородной деформации растяжения или сжатия в одном направлении, или жидкость из анизотропных молекул, помещенная в однородное электрическое поле, также будут оптически одноосными.

В кристаллах более низкой симметрии (триклинная, моноклинная, ромбическая системы) все три главных значения тензора 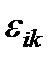различны. Можно показать, что в этом случае существует два направления (оптические оси), вдоль которых обе волны с ортогональными поляризациями распространяются с одной скоростью.

Р и с. 6.5	Р и с. 6. 6

В кристаллах кубической системы (таких, как каменная соль NaCl, флюорит СаF ₂, алмаз С и т.д.) все три главных направления диэлектрического тензора физически эквивалентны, поэтому главные значения ε_х, ε_у и ε_z одинаковы. Это значит, что тензор ε_ik вырождается в скаляр (векторы и всегда совпадают по направлению) и кристаллы кубической системы в отношении оптических свойств ведут себя как изотропная среда. В отношении других свойств, выражаемых тензорами более высокого ранга (например, упругих), кубические кристаллы анизотропны. Оптическая анизотропия кубических кристаллов появляется только при учете очень слабых эффектов пространственной дисперсии, описываемых тензором четвертого ранга.

Перейдем к исследованию распространения света в оптически одноосных кристаллах. Если свет распространяется вдоль оптической оси z, то при любой его поляризации векторы и лежат в плоскости ху и, как и в изотропной среде, совпадают по направлению, причем 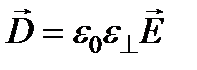. Поэтому скорость волн, распространяющихся вдоль оси, равна 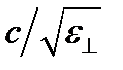, а поляризация может быть любой (линейной, круговой, эллиптической). Ниже будет показано, что в любом другом направлении могут распространяться только линейно поляризованные волны с ортогональными направлениями поляризации, причем скорости этих двух волн различны.

Из-за симметрии выбор направления осей координат в плоскости ху произволен. Воспользуемся этим для упрощения уравнений. Пусть направление луча 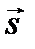(рис. 6.6) составляет некоторый угол θ с оптической осью (осью z). Выберем ось у так, чтобы она лежала в плоскости, образуемой оптической осью и лучом (ее называют плоскостью главного сечения). Тогда вектор 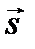имеет следующие проекции: 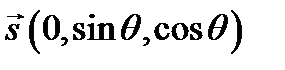. Скалярное произведение 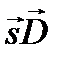в имеет вид sin θD_у +cos θD_z. Выразим проекции в с помощью материальных уравнений, учитывая, что ε_x = ε_y = ε 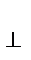, ε_z = ε _║ и запишем в проекциях на оси координат х, у, z: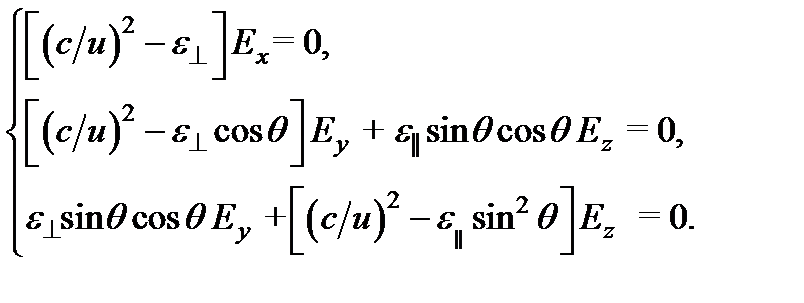

Мы получили систему однородных уравнений для нахождения проекций вектора плоской волны. Система имеет ненулевое решение только тогда, когда ее определитель равен нулю. Это условие и дает уравнение для нахождения лучевой скорости u (θ) при данном направлении луча. Определитель распадается на произведение двух множителей, один из которых равен 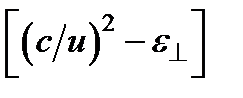. Отсюда сразу находим первый корень уравнения: и = с/ 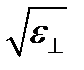= с/п ₀. Подставив его в коэффициенты системы, получим, что у соответствующего этому корню решения проекции напряженности поля Е_у и Е_z тождественно равны нулю, а Е_х может иметь любое значение. Это значит, что описываемая этим решением волна линейно поляризована вдоль оси х, т.е. перпендикулярно оптической оси (и плоскости главного сечения). Ее лучевая скорость и=с/п ₀ не зависит от угла θ, т.е. от направления распространения. Такую волну называют обыкновенной и относящиеся к ней величины снабжают индексом о.

Приравнивая нулю второй множитель в определителе системы, находим еще один корень:

и (θ) = с /(ε 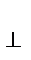cos² θ + 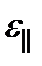sin² θ)^1/2. Подставляя его в коэффициенты системы, находим

.

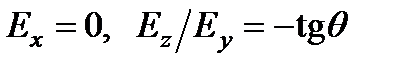Это значит, что распространяющаяся с зависящей от направления (т.е. от угла θ) скоростью и (θ) волна поляризована в плоскости главного сечения, причем вектор перпендикулярен 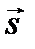(рис. 6.6). Эту волну называют необыкновенной (индекс е). Наряду с главными диэлектрическими проницаемостям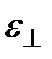и и 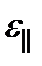для характеристики одноосных сред используют также параметры n ₀ ≡ 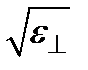и п_е≡ 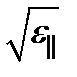, называемые соответственно обыкновенным и необыкновенным показателями преломления.

Других решений система не имеет, т.е. двумя найденными выше волнами с ортогональными линейными поляризациями, имеющими скорости и ₀ = 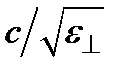=с/п ₀ и и_е (θ), исчерпывается все многообразие нормальных волн, которые могут распространяться по заданному направлению θ.

Для нахождения хода лучей в одноосных кристаллах обычно выполняют геометрические построения, в которых используют поверхности лучевых скоростей (лучевые, или волновые, поверхности). Для построения лучевой поверхности из произвольной точки О во всевозможных направлениях проводят лучи и откладывают на них отрезки, пропорциональные соответствующим значениям лучевой скорости.

Р и с. 6.7

Множество концов отложенных отрезков образует замкнутую поверхность, которая для обыкновенной волны, очевидно, представляет собой сферу радиусом и ₀= 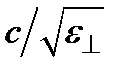, а для необыкновенной волны – эллипсоид вращения с полуосям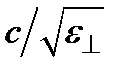и и 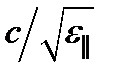. Чтобы убедиться в этом, достаточно переписать соотношение в виде .

Так как и cos θ = и_z, u sin θ = и_y, то ясно, что уравнение определяет эллипсоид вращения в пространстве скоростей, соприкасающийся со сферой для обыкновенной волны в точках, соответствующих направлению оптической оси. Сечение лучевых поверхностей плоскостью yz, проходящей через оптическую ось, показано на рис. 6.7. При п_е>п ₀ (кварц) вытянутый эллипсоид целиком лежит внутри сферы (рис. 6.7, а). Такие кристаллы называют положительными. У отрицательных кристаллов n_e<n ₀ (исландский шпат) и сфера лежит внутри сплющенного эллипсоида (рис. 6.7, б).

Из этих рисунков видно, что при распространении вдоль оптической оси обе волны имеют одинаковую скорость и=с/п ₀, определяемую обыкновенным показателем преломления п ₀. Для этого направления любая плоскость, содержащая оптическую ось, будет плоскостью главного сечения, поэтому возможны как любое направление линейной поляризации, так и в равной мере круговая или эллиптическая поляризация. При распространении в перпендикулярном оптической оси направлении обыкновенная волна имеет по-прежнему скорость и ₀ =с/п ₀, а необыкновенная, в которой вектор направлен вдоль оптической оси, – скорость и_е= 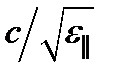=с/п_е, определяемую необыкновенным показателем преломления. Для всех других направлений распространения векторы и не совпадают.