
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Функции plot3d и plot3d1
|
|
Построение трехмерных графиков в SciLab
Рассмотрим основные возможности SciLab по созданию трехмерных графиков: объемных и пространственных. При этом к трехмерным отнесем все графики, положение каждой точки которых задается тремя величинами.
В целом процесс построения графика функции вида 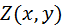 можно разделить на три этапа:
можно разделить на три этапа:
1. Создание в области построения графика прямоугольной сетки. Для этого формируются прямые линии, параллельные координатным осям 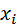 и
и 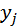 ,
,
где
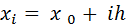 ,
, 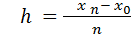 ,
, 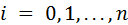 ,
,
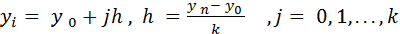
2. Вычисление значений функции 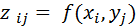 во всех узлах сетки.
во всех узлах сетки.
3. Обращение к функции построения трехмерных графиков.
Функции plot3d и plot3d1
В SciLab поверхность можно построить с помощью функций plot3d или plot3d1. Их отличие состоит в том, что plot3d строит поверхность и заливает ее одним цветом, а plot3d1 -поверхность, каждая ячейка которой имеет цвет, зависящий от значения функции в каждом соответствующем узле сетки.
Обращение к функциям следующее:
plot3d(x, y, z, [theta, alpha, leg,flag,ebox][keyn=valuen]),
plot3d1(x, y, z, [theta, alpha,leg,flag,ebox][keyn=valuen]),
здесь
x -вектор-столбец значений абсцисс;
y -вектор-столбец значений ординат;
z -матрица значений функции;
theta, alpha - действительные числа, которые определяют в градусах сферические координаты угла зрения на график. Попросту говоря, это угол, под которым наблюдатель видит отображаемую поверхность;
leg - подписи координатных осей графика, символы, отделяемые знаком @. Например, ’X@Y@Z’.
flag -массив, состоящий из трех целочисленных параметров: [mode,type,box ].
Здесь
mode - устанавливает цвет поверхности. По умолчанию равен 2 - цвет заливки синий, прямоугольная сетка выводится.
| Значения параметра mode | |
| Значение | Описание |
| > 0 | поверхность имеет цвет «mode», выводится прямоугольная сетка |
| выводится прямоугольная сетка, заливка отсутствует (белый цвет) | |
| < 0 | поверхность имеет цвет «mode», отсутствует прямоугольная сетка |
type - позволяет управлять масштабом графика, по умолчанию имеет значение 2;
| Значения параметра type | |
| Значение | Описание |
| применяется способ масштабирования, как у ранее созданного графика | |
| границы графика указываются вручную с помощью параметра ebox | |
| границы графика определяют исходные данные ebox, определяет наличие рамки вокруг отображаемого графика |
box - определяет наличие рамки вокруг отображаемого графика. По умолчанию равен 4.
| Значения параметра box | |
| Значение | Описание |
| 0 и 1 | нет рамки |
| только оси, находящиеся за поверхностью | |
| выводится рамка и подписи осей | |
| выводится рамка, оси и их подписи |
ebox - определяет границы области, в которую будет выводиться поверхность, как вектор [xmin, xmax, ymin, ymax, zmin,zmax]. Этот параметр может использоваться только при значении параметра type=1.
keyn=valuen -последовательность значений свойств графика key1=value1, key2=value2,..., keyn=valuen, таких как толщина линии, ее цвет, цвет заливки фона графического окна, наличие маркера и др.
Таким образом, функции plot3d (plot3d1) в качестве параметров необходимо передать прямоугольную сетку и матрицу значений в узлах сетки.
Пример 1. Построить график функции 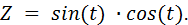
Создадим массив значений аргумента 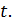 Вычислим значения функции и запишем их в массив
Вычислим значения функции и запишем их в массив 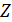 .
.
При обращении к функции plot3d в качестве параметров 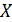 и
и 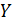 , задающих прямоугольную сетку, дважды указан параметр
, задающих прямоугольную сетку, дважды указан параметр 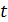 , поскольку обе функции - и sin, и cos зависят от одной переменной
, поскольку обе функции - и sin, и cos зависят от одной переменной 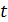
Построение графика функции 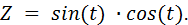 с помощью функции plot3d
с помощью функции plot3d
Теперь немного усложним задачу. Построим поверхность, уравнение которой задается двумя независимыми переменными.
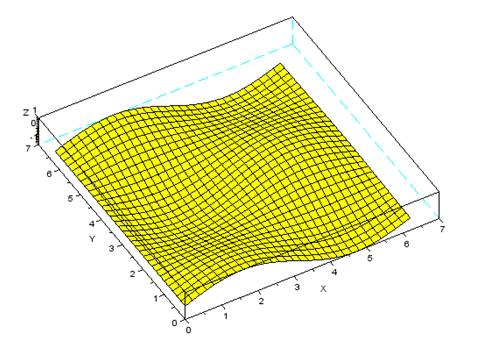
Пример 2. Построить график функции 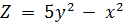 .
.
Прежде всего, зададим массивы 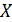 и
и 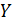 .
.
Затем сформируем матрицу значений функции 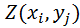 , используя оператор цикла for. Здесь
, используя оператор цикла for. Здесь 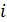 - параметр цикла, который будет перебирать все значения массива
- параметр цикла, который будет перебирать все значения массива 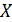 , а
, а 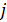 - параметр цикла, который будет сопоставлять каждому значению массива
- параметр цикла, который будет сопоставлять каждому значению массива 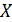 по очереди все значения массива
по очереди все значения массива 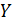 .
.
Таким образом, сначала будут вычислены все значения функции 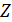 при меняющемся
при меняющемся 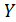 (от первого до последнего значения в массиве) и первом значении массива
(от первого до последнего значения в массиве) и первом значении массива 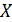 . Затем при втором значении массива
. Затем при втором значении массива 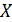 и т. д.
и т. д.
length определяет количество элементов массива 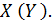
Для построения поверхности обратимся к функции plot3d
x=[-2:0.1:2];y=[-3:0.1:3];for i=1:length(x)for j=1:length(y)z(i,j)=5*y(j)^2-x(i)^2;endendplot3d(x',y',z,120,45,'X@Y@Z',[8,2,4]);// Здесь 35 и 45 угол поворота наблюдателя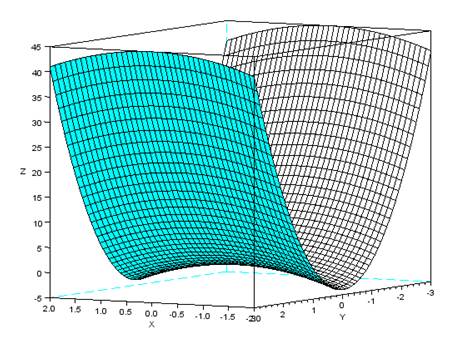
Для построения поверхности обратимся к функции plot3d1
x=[-2:0.1:2];y=[-3:0.1:3];for i=1:length(x)for j=1:length(y)z(i,j)=5*y(j)^2-x(i)^2;endendplot3d1(x',y',z,120,45,'X@Y@Z',[8,2,4]);// Здесь 35 и 45 угол поворота наблюдателя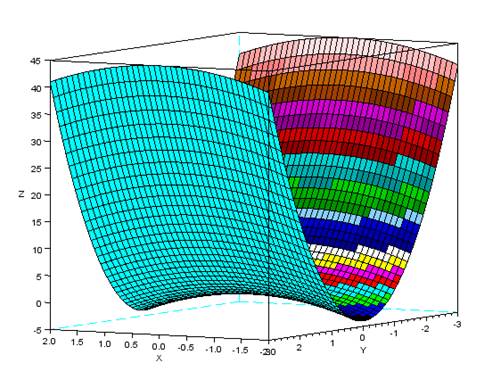
В SciLab существует несколько команд, призванных облегчить процедуру создания прямоугольной сетки - это genfac3d и eval3dp.
Простейшей из них по синтаксису является функция genfac3d:
[xx,yy,zz]=genfac3d(x, y, z)
Здесь xx, yy, zz - результирующая матрица размером (4,(n–1)×(m−1)), где xx(:,i), yy(:,i) и zz(:,i)- координаты каждой из ячеек прямоугольной сетки;
x -вектор x-координат размера m;
y -вектор y-координат размера n;
z -матрица размера (m, n) значений функции 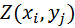
Пример 3. Построить график функции 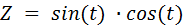 .
.
Определим массив параметра 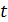 и вычислим значения функции
и вычислим значения функции
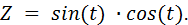
Прямоугольную сетку создадим при помощи команды genfac3d.
Для формирования графика обратимся к функции plot3d.
t=[0:0.3:2*%pi]';z=sin(t)*cos(t');[xx,yy,zz]=genfac3d(t,t,z);plot3d(xx,yy,zz,120,25,'X@Y@Z',[3,2,4]);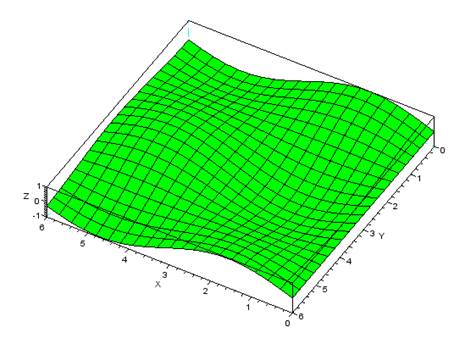
Недостатком команды genfac3d является то, что она все-таки не упрощает работу с функцией plot3d, если поверхность задается функцией от двух переменных.
В таком случае необходимо использовать команду eval3dp:
[Xf,Yf,Zf]=eval3dp(fun,p1,p2)
Xf,Yf,Zf - результирующая матрица размером (4,(n−1)×(m−1)), где xx(:,i),yy(:,i) и zz(:,i)- координаты каждой из ячеек прямоугольной сетки;
fun -функция, определенная пользователем, которая задает трехмерный график;
p1 -вектор размера m;
p2 -вектор размера n.
Проиллюстрируем действие команды eval3dp следующим примером.
Пример 4. Построить график, заданный системой уравнений:
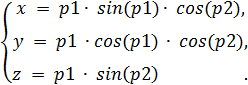
Прежде всего, определим массивы значений параметров p1 и p2. Далее создадим функцию scp, которая задает график.
Функции в SciLab создаются при помощи команды deff:
deff([s1,s2,...]=newfunction(e1,e2,...))
где s1, s2,. - список выходных параметров, т.е. переменных, которым будет присвоен конечный результат вычислений;
newfunction - имя создаваемой функции, оно будет использоваться для ее вызова;
e1, e2,... - входные параметры.
Запишем команду deff в три строки для удобства чтения листинга
Для формирования значений воспользуемся функцией linspace
Функция. linspace(x1, x2), генерирует вектор линейно равноудаленных точек между x1 и x2.
[v]=linspace (x1, x2 [, n])
x1,x2 - вещественные или комплексные значения
n -целое (количество значений)
v - вещественный или комплексный вектор результатов (значение по умолчанию = 100)
p1=linspace(0,2*%pi,10);p2=linspace(0,2*%pi,10);deff("[x,y,z]=scp(p1,p2)",["x=p1.*sin(p1).*cos(p2)";"y=p1.*cos(p1).*cos(p2)";"z=p1.*sin(p2)"]);[Xf,Yf,Zf]=eval3dp(scp,p1,p2);plot3d(Xf,Yf,Zf);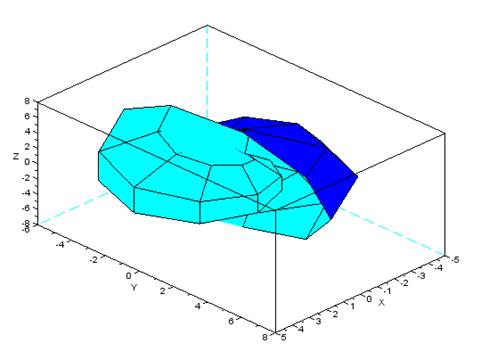
Date: 2015-07-27; view: 2689; Нарушение авторских прав