Оценка точности результатов моделирования

Входные параметры модели часто задаются вероятностно (в виде определенного интервала). Генератор псевдослучайных чи­сел, встроенный в известные системы имитационного моделирова­ния, определяет какое-либо значение параметра (например, посту­пление транзактов) внутри этого интервала. Наличие генератора является источником погрешности имитации.

Поэтому проводят несколько прогонов модели (обычно N = 10) при одних и тех же серединных значениях параметров X, но разных пограничных точках интервалов (например, интервала по­ступления транзактов в блоке GENERATE). По полученным от­кликам (Y) оценивается погрешность. Оценить погрешность мож­но путем определения оценок математического ожидания и дис­персии отклонения компонент вектора откликов Y (применяется понятие «оценка математического ожидания», а не «математиче­ское ожидание», так как речь идет о выборочной совокупности, приблизительно, оценочно отражающей генеральную совокуп­ность). Оценка математического ожидания (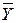) вычисляется по формуле:

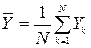(1)

где 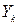- отклики модели по прогонам, N - число прогонов. Оценка дисперсии вычисляется по формуле:

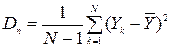(2)

Далее определяется доверительный интервал математическо­го ожидания отклика Y.

Так как погрешности порождаются генераторами псевдослу­чайных чисел, можно допустить нормальный закон распределения отклонений 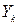от значений Y. Так как выборка является малой (k < 30), то для нахождения доверительных интервалов используется t -статистика (распределение Стьюдента). Алгоритм нахождения доверительного интервала (интервала, в котором с выбранной исследователем вероятностью находится математическое ожидание зна­чений отклика) следующий:

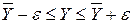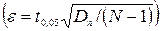, 3)

где 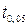- табличное значение, определяемое по таблице «Зна­чения коэффициента 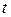-Стьюдента» (оно зависит от числа степеней свободы (v = N -1) и уровня значимости суждений a = 0,05).

Date: 2015-07-27; view: 793; Нарушение авторских прав