
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 8. Статистические методы изучения взаимосвязей
|
|
Связи между явлениями, их признаками подразделяются по степени тесноты связи, по направлению и аналитическому выражению.
По степени тесноты выделяют два типа связей:
функциональные (жестко детерминированные), в которых определенному значению факторного признака соответствует строго определенное значение результативного признака;
стохастические, в которых зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений.
Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
По направлению выделяют связь прямую и обратную; по аналитическому выражению – линейную и нелинейную (криволинейную).
Простейшими методами изучения стохастических связей являются: сопоставления (приведения) параллельных рядов, аналитических группировок, графический. Эти методы позволяют определить лишь направление и характер связи, выявить ее форму.
Для получения количественных оценок связи используется корреляционный и регрессионный анализ.
Корреляционный анализ состоит в оценке тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Регрессионный анализ заключается в определении аналитического выражения зависимости, т.е. в построении модели связи.
Построение регрессионной модели проходит несколько этапов: предварительный теоретический анализ, определение объекта, отбор факторов, сбор и подготовка информации, выбор модели связи, исчисление показателей тесноты корреляционной связи, оценка адекватности регрессионной модели.
Для построения регрессионной модели при парной зависимости могут использоваться следующие виды уравнений:
- прямой: y = a0 + a1x
- параболы: y = a0 + a1x + a2x2
- гиперболы: y = a0 + и др.
Параметры уравнений определяются путем решения системы нормальных уравнений, полученных методом наименьших квадратов.
Для оценки тесноты связи входе корреляционного анализа применяются: линейный коэффициент корреляции, теоретическое корреляционное отношение, индекс корреляции.
Линейный коэффициент корреляции применяется для измерения тесноты связи только при линейной форме связи и вычисляется по формулам:
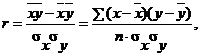 и др.
и др.
Теоретическое корреляционное отношение и индекс корреляции применяются для измерения тесноты корреляционной связи между признаками при любой форме связи, как линейной, так и нелинейной и по формулам:
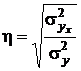 ,
, 
Для упрощения расчетов меры тесноты корреляционной связи часто применяется индекс корреляционной связи, который определяется по следующим формулам:
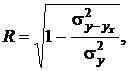
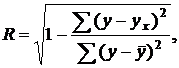
Показателем тесноты связи, устанавливаемой между результативными и двумя или более факторными признаками, является совокупный коэффициент множественной корреляции 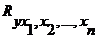 .
.
Важную информацию об исследуемых зависимостях получают в процессе расчета коэффициентов регрессии, эластичности, β – коэффициентов.
Оценку значимости параметров корреляционно-регрессионного анализа осуществляют на основе критериев Стьюдента и Фишера.
Для изучения связи между качественными (атрибутивными) признакамиприменяются непараметрические методы.
Для оценки тесноты связи между альтернативными признаками используют:
коэффициент контингенции:
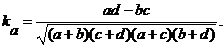
коэффициент ассоциации:
ka = (ad – bc): (ad + bc)
Если по каждому из взаимосвязанных признаков выделяется число групп более двух, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с помощью показателя взаимной сопряженности А.А. Чупрова:
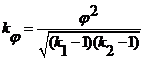
Среди непараметрических методов оценки тесноты связи большое значение имеют ранговые коэффициенты Спирмена и Кендалла, которые могут быль использованы для определения тесноты связи как между количественными, так и между качественными признаками.
Решение типовых примеров
Пример 1
Имеются выборочные данные по 10 однородным предприятиям.
№ предприятия..........………….………… 1 2 3 4 5 6 7 8 9 10
Электровооруженность труда на
одного рабочего, кВт-ч ....… ….………….. 2 5 3 7 2 6 4 9 8 4
Выпуск готовой продукции
на одного рабочего, т.....…………………...3 6 4 6 4 8 6 9 9 5
Построить однофакторную регрессионную модель.
Решение. Предположим, что между электровооруженностью труда и выпуском готовой продукции существует линейная корреляционная связь, которую можно выразить уравнением прямой вида
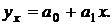
Факторным признаком является электровооруженность труда, а результативным – выпуск готовой продукции.
Для определения формы корреляционной связи необходимо вычислить параметры уравнения прямой путем решения системы нормальных уравнений. Чтобы заполнить систему нормальных уравнений фактическими данными, необходимо определить S xy, S x 2, S y 2.
Расчеты этих показателей произведем в табл. 1.
Таблица 1- Расчет сумм для вычисления параметров уравнения прямой по несгруппированным данным
| Исходные данные | Расчетные значения | ||||||
| № предприятия | Электровооруженоость труда на одного рабочего, кВт×ч х | Выпуск продукции на одного рабочего, т y | ху | х 2 | у 2 | ух |
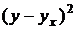
|
| … | … | … | … | … | … | 3,61 6,01 4,41 … 8,38 5,20 | 0,3721 0,0001 0,1682 … 0,381 0,04 |
| Итого | 5,761 | ||||||
| В среднем | 5,0 | 6,0 | 34,3 | 30,4 | 40,0 | 6,0 | 0,5761 |
Подставим в систему нормальных уравнений фактические данные из таблице 1 и получим равенства
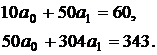
Систему нормальных уравнений решаем в такой последовательности (по методу множителей): умножим каждый член первого уравнения на число, равное 5. Получим
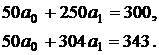
Затем вычтем из второго уравнения первое: 43 = 54 а 1, откуда а 1 = 43 / 54 = 0,7963.
После подстановки значения а 1 в первое уравнение получим а 0 = 2,02.
Уравнение регрессии имеет вид 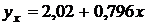 .
.
В нашем уравнении регрессии параметр а 1 = 0,796 показывает, что с увеличением электровооруженности труда одного рабочего на 1 кВт/ч выпуск готовой продукции возрастет на 0,796 т.
Средний коэффициент эластичности:
`Э = 0,796 × 5/6 = 0,66.
Коэффициент эластичности, равный 0,66 показывает, что с увеличением электровооруженности труда на 1% выпуск готовой продукции возрастет на 0,66%.
Измерим тесноту корреляционной связи между производительностью и электровооруженностью труда линейным коэффициентом корреляции, теоретическим корреляционным отношением, индексом корреляции. Данные, необходимые для расчета этих показателей, представлены в табл. 1.
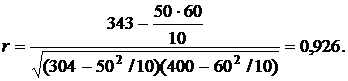
Для расчета теоретического корреляционного отношения необходимо предварительно вычислить дисперсии 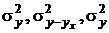 по формулам:
по формулам:
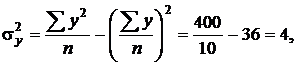

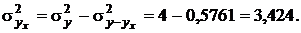
Теоретическое корреляционное отношение равно
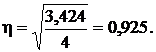
Коэффициент детерминации h2 равен 0,856. Индекс корреляции
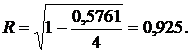
Все показатели тесноты корреляционной связи показывают тесную связь между производительностью и электровооруженностью труда. Коэффициент детерминации 0,856 означает, что вариация выработки рабочих на 85,6% объясняется вариацией электровооруженности труда и на 14,4% - прочими факторами.
Так как r = R =η, то можно сделать заключение, что гипотеза о линейной форме связи подтверждена.
Проведем оценку адекватности регрессионной модели ух = 2,02 + 0,796 х, выражающей зависимость между производительностью и электровооруженностью труда, с помощью F-критерия Фишера.

Табличное значение FТ с уровнем значимости 0,05 и числом степеней свободы (2 - 1), (10 - 2) равно 5,32. Так как FЭ > FТ, то уравнение регрессии можно признать адекватным.
Оценим значимость параметров уравнения регрессии с помощью t -критерия Стьюдента

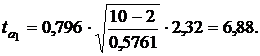
Значение s х равно
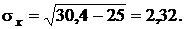
Табличное значение t -критерия с уровнем значимости 0,05 и числом степеней свободы (n - 2) равно 2,307. Так как t эмп > t табл,параметры уравнения регрессии можно признать значимыми.
Значимость коэффициента корреляции оценим с помощью t- критерия
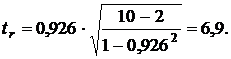
Эмпирическое значение t больше табличного, следовательно, коэффициент корреляции можно признать значимым.
Вычислим ошибку аппроксимации по формуле

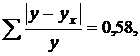
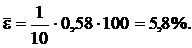
Так как параметры уравнения регрессии значимы, уравнение значимо, показатели тесноты значимы, ошибка аппроксимации равна 5,8%, коэффициент детерминации равен 0,856, то можно сделать заключение, что построенная регрессионная модель зависимости производительности труда от его электровооруженности ух = 2,02 + 0,796 х может быть использована для анализа и прогноза.
Пример 2
Имеются данные по 52 предприятиям отрасли.
| Группа заводов по вооруженности, млн. руб., х | Количество заводов, f | Объем продукции, млн. руб., у |
| 5-7 7-9 9-11 … 21-23 23-25 | … | 3,0 5,0 6,3 … 17,0 19,0 |
По исходным данным найти параметры линейного корреляционного уравнения, характеризующего зависимость между продукцией и фондовооруженностью.
Решение. Расчетные данные для вычисления параметров уравнения регрессии представлены в табл. 2.
Таблица 2 - Расчет сумм для вычисления параметров уравнения прямой по сгруппированным данным
| х | `x | f | `yi | `yif | xf | yi`xf | 
|
| 5-7 7-9 9-11 … 21-23 23-25 | … | … | 3,0 5,0 6,3 … 17,0 19,0 | 3,0 10,0 18,9 … 34,0 19,0 | … | 18,0 80,0 189,0 … 748,0 456,0 | … |
| Итого | - | - | 550,2 | 8641,2 |
Расчетные данные из табл.2 подставим в формулы и определим параметры а 0, а 1:
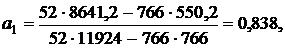
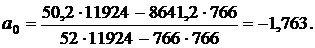
Параметр а 1 показывает, что с ростом фондовооруженности на 1 млн. руб. объем произведенной продукции увеличивается на 0,838 млн. руб.
Уравнение регрессии имеет вид

Тесты
1. Признаки, обуславливающие изменение других, связанных с ними признаков и характеризующие причины этого изменения называются:
а) факторными;
б) результативными.
1) а; 2) б.
2. Признаки, характеризующие следствие изменения под влиянием других, связанных с ними признаков называются:
а) факторными;
б) результативными.
1) а; 2) б.
2. Если каждому возможному значению независимого признака соответствует одно или несколько строго определенных значений зависимого признака, то такая связь называется:
а) стохастической; б) функциональной.
1) а; 2) б.
3. При функциональной зависимости каждому значению признака соответствует:
а) единственное значение результативного признака;
б) множество значений результативного признака;
в) распределение единиц совокупности по результативному признаку;
г) среднее значение результативного признака.
1) а; 2) б; 3) в; 4) г
4. При изменении значений факторного признака функциональная зависимость проявляется в изменении:
а) значений результативного признака;
б) распределения единиц совокупности по результативному признаку;
в) распределения единиц совокупности по факторному признаку;
г) средних значений результативного признака
1) а; 2) б; 3) в; 4) г
5. При изменении значений факторного признака корреляционная зависимость проявляется в изменении:
а) значений результативного признака;
б) распределения единиц совокупности по результативному признаку;
в) распределения единиц совокупности по факторному признаку;
г) средних значений результативного признака
1) а; 2) б; 3) в; 4) г
6. Для корреляционных связей характерно:
а) с изменением значения одной из переменных, другая изменяется строго определенным образом
б) разным значениям одной переменной соответствуют различные средние значения другой
в) связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более.
1) а; 2) б;3) в
7. Для функциональных связей характерно:
а) с изменением значения одной из переменных, другая изменяется строго определенным образом
б) разным значениям одной переменной соответствуют различные средние значения другой
в) связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более.
1) а; 2) б; 3) в
8. Функциональную связь можно представить уравнением:
а) xi = f (y i)
б) y i= f(xi)
в) 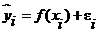
1) а; 2) б; 3) в
9. Стохастическую связь можно представить уравнением:
а) xi = f (y i)
б) y i= f(xi)
в) 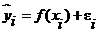
1) а; 2) б; 3) в
10. Теснота связи двух признаков при нелинейной зависимости определяется по формуле…
а) 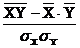
б) 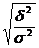
в) 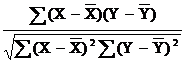
а) 1; б) 2; в) 3.
11. Для аналитического выражения нелинейной связи между факторами используются формулы:
а) 
б) 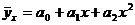
в) 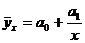
1) а, б; 2) а, в; 3) б, в
12. Прямолинейная связь между факторами исследуется с помощью уравнения регрессии
а) 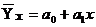
б) 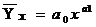
в) 
г) 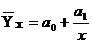
1) а; 2) б; 3) в; 4) г
13. Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле:
а) 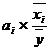 ; б)
; б) 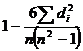 ; в)
; в) 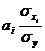 ; г)
; г) 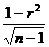
1) а; 2) б; 3) в; 4) г
14. Бета-коэффициент рассчитывается по формуле:
а) 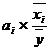 ; б)
; б) 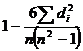 ; в)
; в) 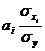 ; г)
; г) 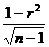
Date: 2015-07-27; view: 4690; Нарушение авторских прав