
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 5. Средние величины и показатели вариации
|
|
Средняя величина – это обобщающая характеристика совокупности однотипных явлений по изучаемому признаку.
Различают степенные и структурные средние.
Степенные средние объединяются общей формулой (при различных значениях m):
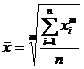
где 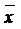 - среднее значение исследуемого явления;
- среднее значение исследуемого явления;
m - показатель степени средней; х - текущее значение (вариант) осредняемого признака; n - число признаков.
В зависимости от значения показателя степени m различают следующие виды степенных средних:
| Значение m | Вид средней величины | Формула расчета | |
| для несгруппированных данных | для сгруппированных данных | ||
| m = -1 | средняя гармоническая | 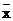 = =
| 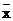 = = 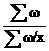
|
| m = 0 | средняя геометрическая | 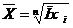
| 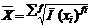
|
| m = 1 | средняя арифметическая | 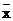 = =
| 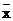 = =
|
| m = 2 | средняя квадратическая | 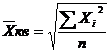
| 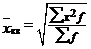
|
| m = 3 | средняя кубическая | 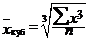
| 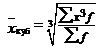
|
Средние показатели могут рассчитываться по дискретным и интервальным рядам. В интервальных рядах для расчета средней определяются середины интервалов.
К структурным среднимотносятся мода и медиана.
Мода – наиболее часто встречающаяся варианта. Для дискретных рядов модой будет значение варианты с наибольшей частотой.
Для интервальных рядов с равными интервалами мода определяется по формуле:
M0 = Xм0 + iм0 .,
где Хмо – начальное значение интервала, содержащего моду;
iм0 – величина модального интервала;
fм0 – частота модального интервала;
fм0-1, fм0+1 – частота интервала, предшествующего модальному, следующего за модальным, соответственно.
Медиана – варианта, расположенная в середине вариационного ряда.
Если ряд дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда. Если ряд имеет четное число членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда.
Медиана интервального ряда определяется по формуле:
Ме = Хме + iме .,
где Хме – начальное значение интервала, содержащего медиану;
iме – величина медианного интервала;
Σf – сумма частот ряда;
Sме-1 – сумма накопленных частот, предшествующих медианному интервалу;
fме – частота медианного интервала.
Для оценки уровня вариации признака в совокупности используются следующие показатели вариации:
| Вид показателя вариации | Формула расчета | |
| для несгруппированных данных | для сгруппированных данных | |
| Размах вариации | R = Xmax – Xmin | |
| Среднее линейное отклонение | d = | d = |
| Дисперсия | σ2 = | σ2 = σ2 = - |
| Среднее квадратическое отклонение | 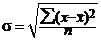
| 
|
| Коэффициент вариации | 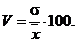
| 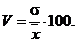
|
Решение типовых примеров
Пример 1
Результаты обследования показали следующее распределение работников торговли по стажу, представленное в табл.1.
Таблица 1 - Распределение работников торговли по стажу работы
| Стаж, лет | Число работников, чел |
| до 6 | |
| 6 - 12 | |
| 12 - 18 | |
| 18 - 24 | |
| св. 24 | |
| ИТОГО |
На основании этих данных исчислить:
1) средний стаж работников торговли;
2) дисперсию и среднее квадратическое отклонение;
3) коэффициент вариации;
Средний стаж работников торговли для открытого интервального ранжированного ряда определим следующим образом.
1. Определим середину каждого интервала Х. Нижнюю границу первого открытого интервала определим условно, используя величину последующего 2- го интервала.
d = 12 - 6 = 6 лет, тогда по 1 интервалу нижняя граница определяется так: 6 - 6 = 0. Середина первого интервала: (0 + 6): 2 = 3 года; середина второго интервала (6 + 12): 2 = 9 лет и т.д. Верхнюю границу открытого последнего интервала определяем по величине предыдущего интервала d = 24-18 = 6, 24 + 6 = 30 лет.
Середина последнего интервала равна (24 + 30): 2 = 27 лет.
2. Средний стаж работников торговли определим по средней арифметической взвешенной
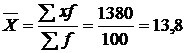 года.
года.
Расчеты оформим в табл. 2 в 3 и 4 графах.
Таблица 2
| Стаж, лет | Число работн., f | х | хf | х - 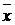
| (х - 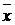 )2 )2
| (х- 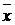 )2 f )2 f
|
| До 6 | -10,8 | 116,64 | 1749,6 | |||
| 6 - 12 | -4,8 | 23,04 | 576,0 | |||
| 12 - 18 | 1,2 | 1,44 | 50,4 | |||
| 18 - 24 | 7,2 | 51,84 | 777,6 | |||
| св. 24 | 13,2 | 174,24 | 1742,4 | |||
| ИТОГО | - | - | - | 4896,0 | ||
| å f | å хf | 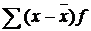
|
Чтобы исчислить дисперсию по формуле 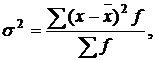 продолжим расчет показателей в табл. 6 графа 5; графа 6; графа 7. Итог графы 7 подставим в формулу для дисперсии:
продолжим расчет показателей в табл. 6 графа 5; графа 6; графа 7. Итог графы 7 подставим в формулу для дисперсии:
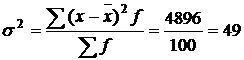 (лет).
(лет).
3. Среднее квадратическое отклонение исчислим по формуле:
 (лет)
(лет)
4. Коэффициент вариации показывает отклонение от среднего значения в среднем, выраженное в процентах, и определяется по формуле:
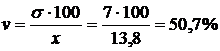
Тесты
1. Средней величиной в статистике называется показатель:
а) стоящий в середине вариационного ряда распределения;
б) характеризующий динамику изучаемого явления;
в) характеризующий типичный уровень явления;
г) отражающий величину варьирующего признака в расчете на единицу совокупности;
д) наиболее часто встречающийся в совокупности;
е) характеризующий многообразие величины признака у отдельных единиц совокупности.
1) а, е; 2) в, г; 3) б, д
2. Правило мажорантности средних определяется как:
а) 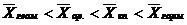
б) 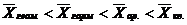
в) 
где 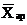 - средняя арифметическая;
- средняя арифметическая;
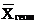 - средняя геометрическая;
- средняя геометрическая;
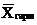 - средняя гармоническая;
- средняя гармоническая;
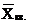 - средняя квадратическая.
- средняя квадратическая.
1) а; 2) б; 3) в
3. Вариация признака – это:
а) изменение массовых явлений во времени;
б) изменение структуры статистической совокупности в пространстве;
в) изменение значений признака во времени и в пространстве;
г) многообразие величины признака у отдельных единиц совокупности.
1) а; 2) б; 3) в; 4) г.
4. Модой в ряду распределения является:
а) наибольшая частота;
б) наибольшая варианта;
в) варианта, которая чаще других встречается в совокупности;
г) варианта, делящая ряд значений признака на две равные части.
1) а; 2)б; 3) в; 4) г.
5. Медианой в ряду распределения является:
а) наибольшая частота;
б) варианта, которая чаще других встречается в совокупности;
в) наибольшая варианта;
г) варианта, делящая ряд значений признака на две равные части.
1) а; 2)б; 3) в; 4) г.
6. Средняя гармоническая простая рассчитывается по формуле:
а) 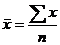 ; б)
; б) 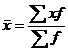 ; в)
; в) 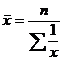 ; г)
; г) 
1) а; 2) б; 3) в; 4) г
7. Средняя арифметическая простая рассчитывается по формуле:
а) 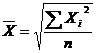 ; б)
; б) 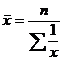 ; в)
; в) 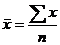 ; г)
; г) 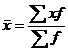
1) а; 2) б; 3) в; 4) г
8. Средняя гармоническая взвешенная рассчитывается по формуле:
а) 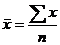 ; б)
; б) 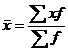 ; в)
; в) 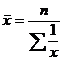 ; г)
; г) 
1) а; 2) б; 3) в; 4) г
9. Средняя арифметическая взвешенная рассчитывается по формуле:
а) 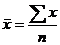 ; б)
; б) 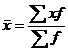 ; в)
; в) 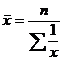 ; г)
; г) 
1) а; 2) б; 3) в; 4) г
10. Недостающим элементом формулы медианы для интервального ряда является:
Ме = Хме + … .
1) 0,5fме; 2) iме ; 3) f; 4) Sме+1
11. Недостающим элементом формулы медианы для интервального ряда является:
Ме = … + iме.
1) 0,5fме; 2) Хме ; 3) f; 4) Sме+1
12. Недостающим элементом формулы моды для интервального ряда является:
M0 = … + iм0 .
1) 0,5fмо; 2) Σf; 3) Хмо 4) Sмо+1
13. Недостающим элементом формулы моды для интервального ряда является:
M0 = Хмо+ … .
1) 0,5fмо; 2) Σf; 3) iм0 ; 4) Sмо+1
14. Размах вариации рассчитывается по формуле:
а) 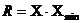 ; б)
; б) 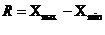 ; в)
; в) 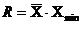 ; г)
; г) 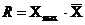
1) а; 2) б; 3) в; 4) г
15. Формулы для расчета среднего линейного отклонения:
а) 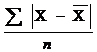 ; б)
; б) 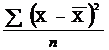 ; в)
; в) 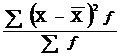 ; г)
; г) 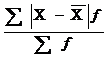 ;
;
д) 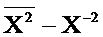
1) а, д; 2) б, в; 3) а,г;
16. Дисперсия рассчитывается по формуле:
а) 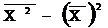 ; б)
; б) 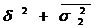 ; в)
; в) 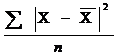 ; г)
; г) 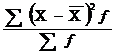
д) 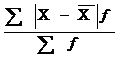
1) а, д; 2) б, в; 3) а, г;
17. Согласны ли Вы с утверждением, что если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая не изменится
1) да; 2) нет
18. Согласны ли Вы с утверждением, что если веса всех осредняемых вариантов уменьшить или увеличить в k раз, то средняя арифметическая не изменится.
1) да; 2) нет
19. Согласны ли Вы с утверждением, что если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака не изменится
20. Если все индивидуальные значения признака уменьшить на 20 единиц, то средняя:
а) уменьшится на 20;
б) уменьшится в 20 раз;
в) не изменится;
г) изменение средней предсказать нельзя.
1) а; 2)б; 3) в; 4) г.
21. Если все индивидуальные значения признака увеличить в 10 раз, то средняя:
а) увеличится на 10;
б) увеличится в 10 раз;
в) не изменится;
г) изменение средней предсказать нельзя.
1) а; 2) б; 3) в; 4) г.
22. Если все индивидуальные значения признака уменьшить в 6 раз, а частоты увеличить в 2 раза, то средняя величина:
а) увеличится в 2 раза;
б) уменьшится в 3 раза;
в) уменьшится в 6 раз;
г) изменение средней предсказать невозможно.
1) а; 2) б; 3) в; 4) г.
23. Если все индивидуальные значения признака уменьшить в 8 раз, а частоты увеличить в 2 раза, то средняя величина:
а) увеличится в 2 раза;
б) уменьшится в 4 раза;
в) уменьшится в 8 раз;
г) изменение средней предсказать невозможно.
1) а; 2) б; 3) в; 4) г.
24. Средняя величина признака равна 20, а коэффициент вариации - 25%.
Дисперсия признака равна:
1) 25; 2) 5; 3) 50.
25. Коэффициент вариации равен 50%, дисперсия признака -36. Средняя величина признака равна:
1) 72; 2) 12; 3) 72
Date: 2015-07-27; view: 4354; Нарушение авторских прав