Венгерский алгоритм

Сущность венгерского алгоритма состоит в том, чтобы в исходной матрице c_ijполучить т=п независимых нулей, т. е. чтобы в каждой строке или столбце должен быть только один ноль.

Шаг 1. Редукция строк и столбцов.

Цель данного шага состоит в получении максимально возможного числа нулевых элементов в матрице стоимостей. Для этого из всех элементов каждой строки вычитают минимальный элемент соответствующей строки, а затем из всех элементов каждого столбца полученной матрицы вычитают минимальный элемент соответствующего столбца. В результате получают редуцированную матрицу стоимостей и переходят к поиску назначений.

Шаг 2. Модификация редуцированной матрицы.

Для редуцированной матрицы стоимостей:

а) Вычеркнуть все строки и столбцы, содержащие максимальное количество нулей. Далее, двигаясь по строкам (сверху вниз) и по столбцам (слева направо) вычёркиваем соответственно строки, а потом столбцы, содержащие нулевые элементы.

б) В полученной сокращённой матрице выбираем минимальный элемент и:

- вычитаем его из всех не вычеркнутых элементов;

- прибавляем его к элементу, расположенному на пересечении двух линий.

Шаг 3. Проверяем план на оптимальность.

Если он не оптимальный, повторяем процедуры шага 2.

Примечания

1) Если число линий, необходимое для того, чтобы вычеркнуть нулевые элементы, равно числу строк (столбцов), то существует полное назначение.

2) Если исходная задача является задачей максимизации, то все элементы матрицы стоимостей следует умножить на(- 1) и сложить их с достаточно большим числом так, чтобы матрица не содержала отрицательных элементов. Затем задачу следует решать как задачу минимизации.

Покажем работу венгерского алгоритма на примере задачи о назначениях со следующей матрицей стоимостей:

min

С = (c_ij) =

Необходимо направить ресурсы на объекты так, чтобы суммарная стоимость была минимальна

Итерация 1.

Шаг 1. Редукция строк и столбцов.

Значения минимальных элементов строк 1, 2, 3 и 4 равны 2, 4, 11 и 4 соответственно. Вычитая из элементов каждой строки соответствующее минимальное значение, получим следующую матрицу:

min 0 0 5 0

Значения минимальных элементов столбцов 1, 2, 3 и 4 равны 0, 0, 5 и 0 соответственно. Вычитая из элементов каждого столбца соответствующее минимальное значение, получим следующую матрицу:

y cy9kb3ducmV2LnhtbEyPwU7DMAyG70i8Q2QkLoilK2UdpemEkDjAGNrGHsBrTFvRJFWTdt3bY05w tP3p9/fnq8m0YqTeN84qmM8iEGRLpxtbKTh8vtwuQfiAVmPrLCk4k4dVcXmRY6bdye5o3IdKcIj1 GSqoQ+gyKX1Zk0E/cx1Zvn253mDgsa+k7vHE4aaVcRQtpMHG8ocaO3quqfzeD0bB22a9fT+km3OC N2ParBcfTr8OSl1fTU+PIAJN4Q+GX31Wh4Kdjm6w2otWwd1DnDCq4D5OQTCQzCNeHJlcpinIIpf/ KxQ/AAAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABb Q29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAA AAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAEh0OdWlAgAAewUAAA4AAAAAAAAAAAAA AAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAF5fy3DhAAAACgEAAA8AAAAAAAAA AAAAAAAA/wQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMAAAANBgAAAAA= " adj="240"/>

=

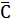В этой матрице в строке 3 и столбце 1 по два нуля, т. е. необходимо провести дальнейшую модификацию редуцированной матрицы стоимостей (оптимальный план не получен).

y cy9kb3ducmV2LnhtbEyPTUvDQBCG74L/YRnBi9hNTUxjzKZowQ8QhKZevG2TMQnuzobstkn/veNJ T8MwD+88b7GerRFHHH3vSMFyEYFAql3TU6vgY/d0nYHwQVOjjSNUcEIP6/L8rNB54yba4rEKreAQ 8rlW0IUw5FL6ukOr/cINSHz7cqPVgdexlc2oJw63Rt5EUSqt7ok/dHrATYf1d3WwCja702OKz5Ov qk97lb29m5fX1Ch1eTE/3IMIOIc/GH71WR1Kdtq7AzVeGAXxapkwqiC55clAnCV3IPZMZnECsizk /wrlDwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAA W0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAA AAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQBEfPI/pQIAAHoFAAAOAAAAAAAAAAAA AAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQCI7YCD4gAAAAoBAAAPAAAAAAAA AAAAAAAAAP8EAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAADgYAAAAA " adj="176"/> Шаг 2. Модификация редуцированной матрицы.

Получим сокращённую матрицу стоимостей:

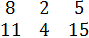- min = 2 =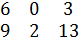

Этот минимум прибавляем к элементам редуцированной матрицы, стоящим на пересечении вычеркнутых строк и столбцов (11, 2). В результате получаем модифицированную матрицу:

Шаг 3. Проверяем полученный план на оптимальность и производим назначения.

Отыскиваем строки с одним нулём и отмечаем его. Это строка 2. Следующая строка-4. Отмечаем нуль в этой строке, одновременно вычёркиваем оставшийся ноль в первом столбце. Следующая строка, содержащая один 0-1, отмечаем этот ноль, одновременно вычёркиваем ноль в 3 столбце. Отмечаем ноль в 4 столбце. Все нули независимы, т. е. получен оптимальный план, накладывая модифицированную матрицу на исходную матрицу стоимости, видим, что все назначения сделали.

0 0 1 0

0 1 0 0

0 0 0 1

1 0 0 0

Оптимальное назначение: Х₁₃=1; Х₂₂=1; Х₃₄=1;Х₄₁=1

Накладываем модифицированную матрицу на исходную, получим F(x)=9+4+11+4=28

Ответ: Первый ресурс направляем на 3-й объект, второй – на 2-й объект, четвертый – на 1-й объект, третий ресурс – на 4-й объект. Стоимость назначения: 9+4+11+4=28.

Примечания 1: Если исходная матрица не является квадратной, то нужно ввести фиктивные ресурсы или фиктивные объекты, чтобы матрица стала квадратной.

Таким образом, суть венгерского метода состоит в следующем: Путем прибавления определенным образом найденных чисел к некоторым столбцам и вычитания из них некоторых чисел находят систему так называемых независимых нулей. Набор нулей называется системой независимых нулей, если никакие два (или более) нуля не лежат на одной линии (в строке или столбце). Если число независимых нулей равно n, то, приняв соответствующие им переменные х_ij равными 1, а все остальные – равными 0, получим оптимальный план назначения.

Date: 2015-07-27; view: 735; Нарушение авторских прав