Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Математическая постановка задачи о назначениях
|
|
Рассмотрим ситуацию, когда требуется распределить m работ (или исполнителей) по пстанкам. Работа i(i=1,…,т), выполняемая на станке j (j=1, …, п), связана с затратами сij. Задача состоит в таком распределении работ по станкам (одна работа выполняется на одном станке), которое соответствует минимизации суммарных затрат.
Эту задачу можно рассматривать как частный случай транспортной задачи. Здесь работы представляют «исходные пункты», а станки-«пункты назначения». Предложение в каждом исходном пункте равно 1, т. е. ai = 1 для всех i. Аналогично спрос в каждом пункте назначения равен 1, т. е. bj = 1 для всех j. Стоимость «перевозки» (прикрепления) работы i к станку j равна cij. Если какую-либо работу нельзя выполнять на некотором станке, то соответствующая стоимость cij берётся равной очень большому числу.
Запишем исходные данные в таблицу.
| Bj Аi | … | n | ai | ||
| c11 | c12 | … | c1n | ||
| c21 | c22 | … | c2n | ||
| … | … | … | … | … | … |
| n | cm1 | cm2 | … | cmn | |
| bj | … |
Прежде чем решать такую задачу, необходимо ликвидировать дисбаланс, добавив фиктивные работы или станки в зависимости от начальных условий. Поэтому без потери общности можно положить m=n.
Пусть xij=0, если j-я работа не выполняется на i-ом станке,
xij=1, еслиj-я работа выполняется на i-ом станке.
Таким образом, решение задачи может быть записано в виде двумерного массива X = (xij). Допустимое решение называется назначением. Допустимое решение строится путём выбора одного элемента в каждой строке матрицы X = (xij) и одного элемента в каждом столбце этой матрицы. Для заданного значения nсуществует n! допустимых решений.
Теперь задача будет формулироваться следующим образом:
xij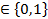 
Ограничения первой группы необходимы для того, чтобы каждая работа выполнялась один раз. Ограничения второй группы гарантируют, что каждому стану будет приписана одна работа.
Для иллюстрации задачи о назначениях рассмотрим таблицу с тремя работами и тремя станками.
Станки
1 2 3
Виды работ 2
3
Специфическая структура задачи о назначениях позволяет использовать эффективный метод для её решения.
Примечание. Оптимальное решение задачи не изменится, если из любой строки или столбца матрицы стоимостей вычесть произвольную постоянную величину (редукция).
Приведённое замечание показывает, что если можно построить новую матрицу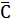 
с нулевыми элементами и эти нулевые элементы или их подмножество соответствуют допустимому решению, то такое решение будет оптимальным:
5 7 9 5 0 2 4 0 2 2
С = 14 10 12 10 4 0 2 4 0 0
15 13 16 13 2 0 3 2 0 1
0 0 2
Оптимальное назначение:
x11*= 1, x23* = 1, x32* = 1, остальные хij* = 0,
F(x*) = 5+12+13 = 30.
Так как задача о назначениях является частным случаем ТЗ, для её решения можно воспользоваться любым алгоритмом линейного программирования, однако более эффективным является венгерский метод (алгоритм).
Date: 2015-07-27; view: 854; Нарушение авторских прав