Свойства плотности распределения

Свойство 1. .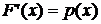

Свойство 2. Плотность распределения—неотрицательная функция: .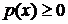

Поскольку F(x)—неубывающая функция, то F’(x)≥0. Следовательно 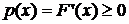—неотрицательная функция.

Геометрически это свойство означает, что график плотности распределения расположен либо над осью ох, либо на этой оси. График плотности распределения называют кривой распределения.

Свойство 3. Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице:

.

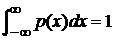В формуле (1) подставим х=+∞, 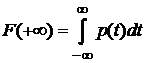. Поскольку 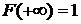, то .

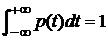Свойство 4. Вероятность того, что непрерывная случайная величина Х примет значение из множества В, равна интегралу по множеству В от плотности распределения.

.

Пример. Задана плотность вероятности случайной величины Х.

.

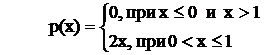Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).

Искомая вероятность .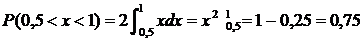

o Говорят, что случайная величина Х равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности:

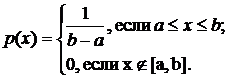
Найдем функцию распределения равномерно распределенной случайной величины X.

а) x<a

;

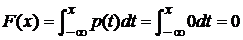б) a≤x≤b

.

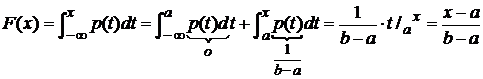в) x>b

.

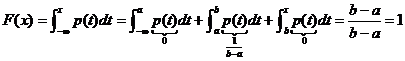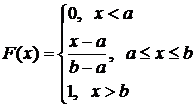
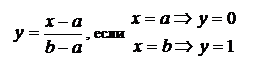
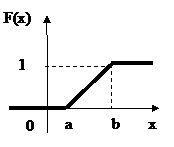
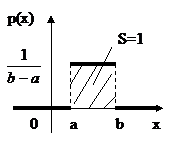
Примером равномерно распределенной случайной величины может служить Х-координата точки, наудачу брошенной на [a, b].

o Говорят, что случайная величина Х имеет показательное (экопоненциальное) распределение с параметром λ>0, если она непрерывна и имеет плотность распределения

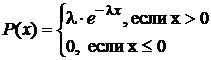; обозначают Х~M(λ).

Найдем функцию распределения показательно распределенной случайной величины Х.

а) x≤0

.

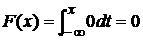б) x>0

.

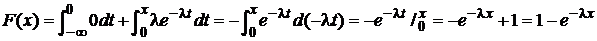Таким образом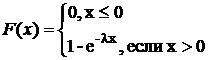

Мы определили показательный закон с помощью плотности распределения. Ясно, что его можно определить, используя функцию распределения.

Пример. Непрерывная случайная величина Х распределена по показательному закону 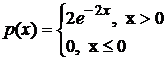. Найти вероятность того, что в результате испытания Х попадет в интервал (0,3; 1).

1. .

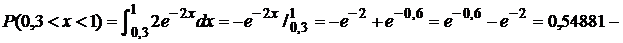
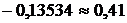2. .

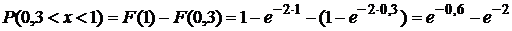o Говорят, что случайная величинf Х имеет нормальное распределение с параметрами a, G², если она непрерывна и имеет плотность 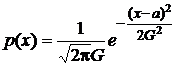. Обозначение Х~N(a, G²), те Х имеет нормальное распределение с параметрами a, G².

График плотности нормально распределенной случайной величины имеет вид:

o Если случайная величина Х~N(0,1), то говорят, что случайная величина Х имеет стандартное нормальное распределение. В этом случае плотность обозначается 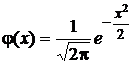. Через N(x) обозначим 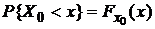, где Х₀~N(0,1).

.

.

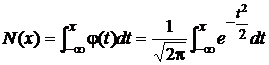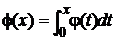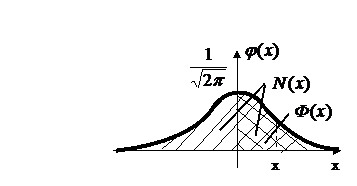
o Любая функция (правило, характеристика), позволяющая вычислить вероятность того, что случайная величина Х принадлежит В—числовому множеству на прямой, т.е. P(X 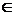B), называется законом распределения случайной величины Х.

1. F(x)—функция распределения является законом распределения любой случайной величины. .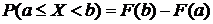

2. Ряд распределения дискретной случайной величины также является законом распределения дискретной случайной величины.

3. Плотность распределения непрерывной случайной величины p(x) является законом распределения непрерывной случайной величины.

.

o Математическим ожиданием или средним значением непрерывной случайной величины Х с плотностью p(x) называется число 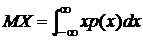при условии, что этот интеграл сходится абсолютно.

Пример 1. Пусть Х имеет равномерное распределение на [a, b].

.

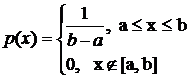
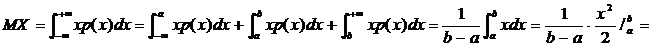
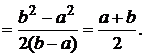
Пример 2. Пусть случайная величина Х~N(a, G²).

Поскольку 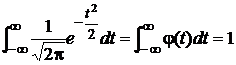. (интеграл от плотности φ(t)).

Таким образом, , т.е. смысл параметра а—математическое ожидание случайной величины Х.

Пример 3. Найти математическое ожидание случайной величины Х, имеющей показательное распределение с параметром λ>0, т.е. X~M(λ)

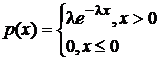
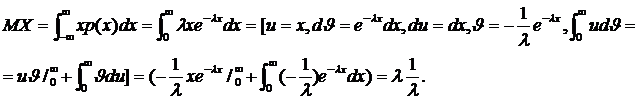
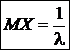
o Дисперсией непрерывной случайной величины Х называется число 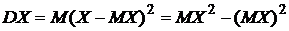. Если случайная величина имеет плотность p(x), .

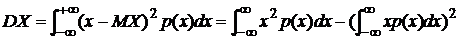Математическоеожидание и дисперсия непрерывных случайных величин обладают теми же свойствами, что и для дискретных случайных величин.

Пример 4. Найти дисперсию случайной величины Х, распределенной равномерно на [a, b]: 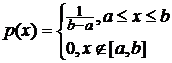. Нашли, что .

.

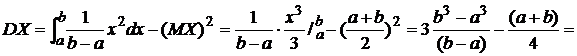
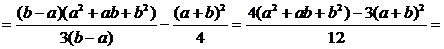
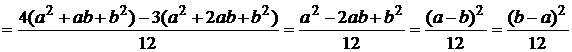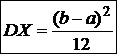
Пример 5. Пусть случайная величина Х имеет нормальное распределение X~N(a, G²). Найти дисперсию DX.

X~N(a, G²). MX=a.

.

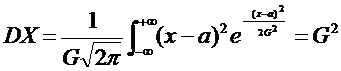Таким образом, .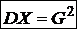

Пример 6. Пусть случайная величина Х имеет показательное распределение 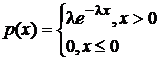. Найти DX.

^.

.

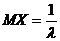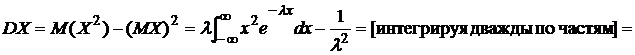
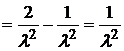Таким образом, .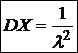

Теорема 1. Если случайная величина Х имеет нормальное стандартное распределение с параметрами (a, G²), то случайная величина 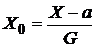имеет нормальное распределение, т.е. .

; .

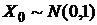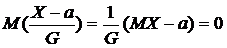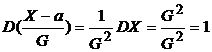Date: 2015-07-27; view: 689; Нарушение авторских прав