
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Числовые характеристики дискретных случайных величин
|
|
Как известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание, которое приближенно равно среднему значению случайной величины.
o Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то 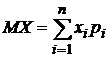 .
.
Если случайная величина Х принимает счетное число значений, то 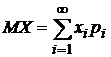 , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание дискретной случайной величины—это неслучайная величина (т.е. число, постоянная).
Пример 1. Найти математическое ожидание случайной величины Х, зная ее ряд распределения.
| X | |||
| P | 0,1 | 0,6 | 0,3 |
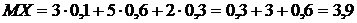 .
.
Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.
Случайная величина Х—число появлений события А в одном испытании, может принимать значения х1=1 (событие А наступило) с вероятностью р и х2=0 (А не наступило) с вероятностью q=1-p.
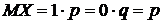 .
.
Таким образом, математическое ожидание числа появлений события в одном испытании равно вероятности это события.
Свойства математического ожидания:
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: M(C)=C.
Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно, 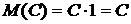 .
.
Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X).
Если случайная величин Х имеет ряд распределения
| X | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
Ряд распределения случайной величины СХ
| СХ | Сx1 | Сx2 | … | Сxn | … |
| Р | p1 | p2 | … | pn | … |
Математическое ожидание случайной величины СХ 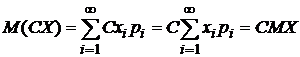 .
.
o Случайные величины X1,X2,…,Xn называются независимыми, если для любых числовых множеств B1,B2,…,Bn 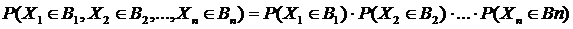 .
.
Если взять B1=]-∞, x1[; B2=]-∞, x2[; …; Bn=]-∞,xn[, то 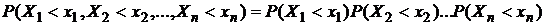 .
.
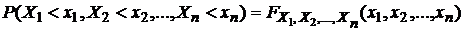 —совместимая функция распределения случайных величин Х1,Х2,…,Хn. Таким образом,
—совместимая функция распределения случайных величин Х1,Х2,…,Хn. Таким образом, 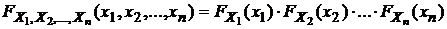 . Данное равенство также можно взять в качестве определения независимости случайных величин.
. Данное равенство также можно взять в качестве определения независимости случайных величин.
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
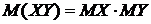 .
.
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
Свойство 4. Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых:
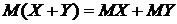 .
.
Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
Пример. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.
Обозначим случайную величину Х—число очков, выпавших на первой кости, через Y обозначим число очков, выпавших на второй кости. Возможные значения этих величин одинаковы и равны 1,2,3,4,5,6, причем вероятность каждого из этих значений равна 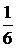 . Найдем математическое ожидание числа очков, которые могут выпасть на первой кости.
. Найдем математическое ожидание числа очков, которые могут выпасть на первой кости.
 . Очевидно, что
. Очевидно, что  .
.
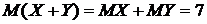 .
.
Теорема 1. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:  .
.
Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события 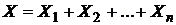 . По свойству 4:
. По свойству 4:
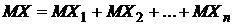 .
.
Согласно примеру 2 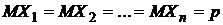 . Таким образом, получим
. Таким образом, получим  .
.
o Дисперсией случайной величины называется число 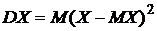 . Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
. Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.
o Средним квадратическим отклонением случайной величины Х называется число 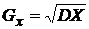 .
.
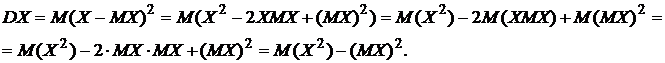
Пример 4. Найти дисперсию случайной величины Х, которая задана рядом распределения.
| X | |||
| P | 0,1 | 0,6 | 0,3 |
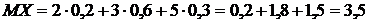 .
.
Ряд распределения случайной величины Х2
| Х2 | |||
| Р | 0,1 | 0,6 | 0,3 |
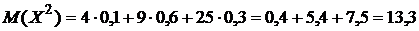
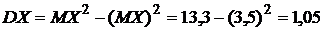 .
.
Date: 2015-07-27; view: 509; Нарушение авторских прав