Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Частные производные высших порядков
|
|
Пусть функция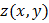 
в некоторой окрестности точки 
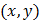имеет частные производные
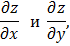
или в других обозначениях
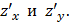
Частные производные являются функциями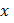 
и 
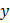, которые, в свою очередь, могут иметь частные производные
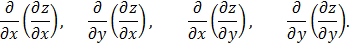
Если это так, то последние называются частными производными 2–го порядка функции 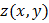и обозначаются соответственно:
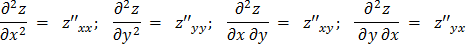
Аналогично определяются частные производные более высоких порядков.
Частные производные, образованные дифференцированием по различным аргументам, называются смешанными частными производными. Например, смешанные производные 2–го порядка функции двух переменных суть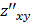 
и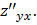 
Среди смешанных производных одного порядка выделяют производные:
1) отличающиеся количеством дифференцирований по одноименным аргументам (например, 
и 
;
2) отличающиеся лишь порядком дифференцирования по аргументам (например, 
).
Теорема о равенстве смешанных частных производных:
Теорема: Если смешанные частные производные, отличающиеся лишь порядком дифференцирования, непрерывны в некоторой точке, то их значения в этой точке равны.
Date: 2015-07-27; view: 402; Нарушение авторских прав